
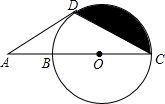
 如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.
如图,B、O是线段AC的三等分点,以O为圆心,OC为半径作⊙O,D为⊙为上一点且DC=DA.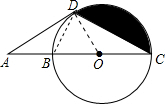 解:(1)AD是⊙O的切线,证明如下:
解:(1)AD是⊙O的切线,证明如下:
|
| 3 |
| 120π×22 |
| 360 |
| 3 |
| 4 |
| 3 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).
如图所示是淮河的一段,两岸AB∥CD,河岸AB上有一排大树.小明为了测量该段河的宽度,先用测角仪在河岸CD的M处测得∠α=33°,然后沿河岸走40米到达N点,测得∠β=64°.请你帮小明算出河宽ER(结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
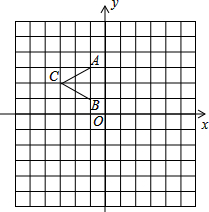 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)查看答案和解析>>
科目:初中数学 来源: 题型:
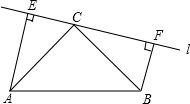 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.查看答案和解析>>
科目:初中数学 来源: 题型:
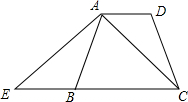 如图,在四边形ABCD中,AD∥BC,且AB=CD,∠D=∠BAD,延长线段CB到E,使BE=AD,连接AE、AC
如图,在四边形ABCD中,AD∥BC,且AB=CD,∠D=∠BAD,延长线段CB到E,使BE=AD,连接AE、AC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com