
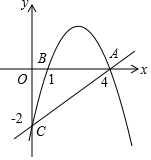
 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.分析 (1)由A与B坐标设出抛物线解析式,将C坐标代入确定出解析式即可;
(2)找出抛物线的顶点坐标与对称轴即可.
解答 解:(1)根据题意设抛物线解析式为y=a(x-4)(x-1),
将C(0,-2)代入得:4a=-2,即a=-$\frac{1}{2}$,
则抛物线解析式为y=-$\frac{1}{2}$(x-4)(x-1)=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2;
(2)抛物线对称轴为直线x=-$\frac{b}{2a}$=-$\frac{\frac{5}{2}}{2×(-\frac{1}{2})}$=$\frac{5}{2}$,顶点坐标为($\frac{5}{2}$,$\frac{9}{8}$).
点评 此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 已知:图中平行于x轴的线段AB上的任意一点的坐标可表示为(x,-3)(-3≤x≤2).
已知:图中平行于x轴的线段AB上的任意一点的坐标可表示为(x,-3)(-3≤x≤2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我们给中国象棋棋盘建立一个平面直角坐标系如图是我市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),请以光岳楼为原点,画出直角坐标系,并用坐标表示下列景点的位置.
如图,我们给中国象棋棋盘建立一个平面直角坐标系如图是我市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),请以光岳楼为原点,画出直角坐标系,并用坐标表示下列景点的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的三边满足a+b=2c | B. | 三角形三边的平方比为3:4:5 | ||
| C. | ∠A+∠B=2∠C | D. | 三角形的三边长为9,40,41 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com