
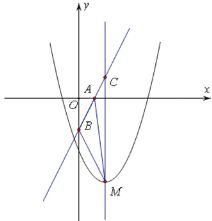
【题目】已知二次函数![]() 的图象( 记为抛物线
的图象( 记为抛物线![]() ) 顶点为M,直线
) 顶点为M,直线![]() :y=2x-a与x轴,y轴分别交于点A,B.
:y=2x-a与x轴,y轴分别交于点A,B.
(1)若抛物线![]() 与x轴只有一个公共点,求a的值;
与x轴只有一个公共点,求a的值;
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系式;
(3)将二次函数![]() 的图象
的图象![]() 绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线
绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线![]() ,顶点为N。
,顶点为N。
①若点N恰好落在直线![]() 上,求a 与t 满足的关系;
上,求a 与t 满足的关系;
②当-2≤x≤1时,旋转前后的两个二次函数y的值都会随x的值得增大而减小,求t 的取值范围.
【答案】(1)a=-2;(2)S=a;(3)①a=2t;②t≤![]() .
.
【解析】
(1)抛物线与x轴只有一个交点,即只有顶点M在x轴上,故M的纵坐标为0;
(2)设直线![]() 与二次函数
与二次函数![]() 的图象
的图象![]() 的对称轴x=1交于点C,则C(1,2-a),根据S=
的对称轴x=1交于点C,则C(1,2-a),根据S=![]() 即可得S与a的函数关系式;
即可得S与a的函数关系式;
(3)①根据题意,点M绕点P(t,-2)旋转180°得到点N,所以MP=NP,即P为MN中点,根据中点坐标公式可得点N的坐标(2t-1,a-2),代入直线![]() :y=2x-a即可求a与t的关系式;
:y=2x-a即可求a与t的关系式;
②旋转前的抛物线对称轴为直线x=1,要满足在-2≤x≤1时y随x的增大而减小,即在对称轴左侧抛物线下降,故开口向上;则旋转后的抛物线开口向下,对称轴必须在x=-2的左侧,即求出t的范围.
解:(1)![]()
抛物线![]() 的顶点M的坐标为(1,-a-2).
的顶点M的坐标为(1,-a-2).
∵二次函数的图象![]() 与x轴只有一个公共点
与x轴只有一个公共点
∴顶点M在x轴上
∴-a-2=0,
∴a=-2 ;
(2)∵y=2x-a与x、y轴分别交于A、B两点
∴A(![]() ,0),B(0,
,0),B(0,![]() )
)
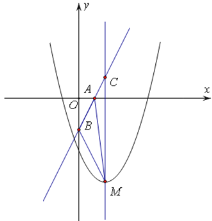
设直线![]() 与二次函数
与二次函数![]() 的图象
的图象![]() 的对称轴x=1交于点C,则C(1,2-a),CM=(2-a)-(-a-2)=4
的对称轴x=1交于点C,则C(1,2-a),CM=(2-a)-(-a-2)=4
∴S=![]() ;
;
(3)①根据题意得,抛物线![]() 的顶点N与抛物线
的顶点N与抛物线![]() 的顶点M关于P(t,-2)成中心对称,
的顶点M关于P(t,-2)成中心对称,
∴顶点N坐标为(2t-1a-2)
∵点N恰好落在直线![]() 上
上
∴a-2=2(2t-1)-a
∴a=2t ;
②∵旋转前抛物线对称轴为直线x=1
∴当a>0抛物线开口向上时,当-2≤x≤1时,抛物线![]() 的y的值随x的值增大而减小
的y的值随x的值增大而减小
∴旋转后抛物线开口向下,且顶点N(2t-1,a-2)
∵要满足在-2≤x<1的范围内y随x增大而减小,即抛物线下降
∴对称轴直线x=2t-1需在x=-2左侧
∴2t-1≤-2
解得:t≤![]()
∴当t≤![]() 时抛物线
时抛物线![]() 的y的值随x的值增大而减小.
的y的值随x的值增大而减小.
故答案为:(1)a=-2;(2)S=a;(3)①a=2t;②t≤![]() .
.


科目:初中数学 来源: 题型:
【题目】(本题满分8分)“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为![]() 米,tanA=
米,tanA=![]() .现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
.现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
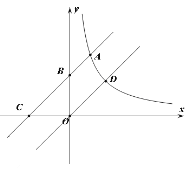
【题目】直线y=kx与反比例函数y=![]() (x>0)的图象相交点D(
(x>0)的图象相交点D(![]() ,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且
,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且![]() ,求平移后的直线的表达式.
,求平移后的直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
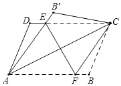
【题目】如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,点D是线段BC上一动点,连接AD,以AD为边作△ADE∽△ABC,点N是AC的中点,连接NE,当线段NE最短时,线段CD的长为_____.
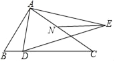
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
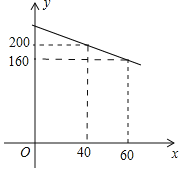
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
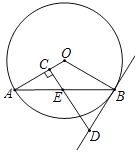
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com