
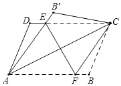
【题目】如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
【答案】(1)见解析(2)见解析
【解析】
(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;
(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.
证明:(1)∵四边形ABCD是平行四边形
∴AD=BC,CD∥AB,∠B=∠D
∵平行四边形ABCD沿其对角线AC折叠
∴BC=B'C,∠B=∠B'
∴∠D=∠B',AD=B'C且∠DEA=∠B'EC
∴△ADE≌△B'EC
(2)四边形AECF是菱形
∵△ADE≌△B'EC
∴AE=CE
∵AE=CE,EF⊥AC
∴EF垂直平分AC,∠AEF=∠CEF
∴AF=CF
∵CD∥AB
∴∠CEF=∠EFA且∠AEF=∠CEF
∴∠AEF=∠EFA
∴AF=AE
∴AF=AE=CE=CF
∴四边形AECF是菱形


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(12,0),O为坐标原点,P是线段OA上任一点(不含端点O、A),二次函数y1的图象过P、O两点,二次函数y2的图象过P、A两点,它们的开口均向下,顶点分别为B、C,射线OB与射线AC相交于点D.则当OD=AD=9时,这两个二次函数的最大值之和等于( )
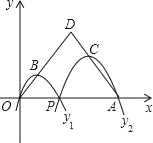
A. 8 B. 3![]() C. 2
C. 2![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全员赛课比赛,八年级3位数学老师分别记为A,B,C,(其中A是女老师,B,C是男老师)被安排在星期二下午三节上,他们通过抽签决定上课顺序。
(1)女老师A不希望上第一节课,却偏偏抽到上第一节课的概率是
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求女老师A比男老师B先上课的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
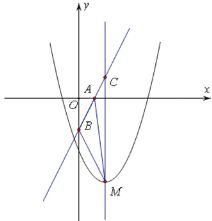
【题目】已知二次函数![]() 的图象( 记为抛物线
的图象( 记为抛物线![]() ) 顶点为M,直线
) 顶点为M,直线![]() :y=2x-a与x轴,y轴分别交于点A,B.
:y=2x-a与x轴,y轴分别交于点A,B.
(1)若抛物线![]() 与x轴只有一个公共点,求a的值;
与x轴只有一个公共点,求a的值;
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系式;
(3)将二次函数![]() 的图象
的图象![]() 绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线
绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线![]() ,顶点为N。
,顶点为N。
①若点N恰好落在直线![]() 上,求a 与t 满足的关系;
上,求a 与t 满足的关系;
②当-2≤x≤1时,旋转前后的两个二次函数y的值都会随x的值得增大而减小,求t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合.展开后,折痕
重合.展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .连接
.连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() .
.
其中正确结论的序号是( )
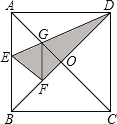
A. ①②③④⑤B. ①②③④C. ①③④⑤D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点A到直线BC的距离为d,AB>AC>d,以A为圆心,AC为半径画圆弧,圆弧交直线BC于点D,过点D作DE∥AC交直线AB于点E,若BC=4,DE=1,∠EDA=∠ACD,则AD=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com