练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校举行全员赛课比赛，八年级3位数学老师分别记为A,B,C,（其中A是女老师，B,C是男老师）被安排在星期二下午三节上，他们通过抽签决定上课顺序。

    （1）女老师A不希望上第一节课，却偏偏抽到上第一节课的概率是

    （2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求女老师A比男老师B先上课的概率．

    【答案】（1）；（2）.

    【解析】

    （1）根据概率公式计算即可求得结果；
    （2）画树状图得出所有等可能结果，再从中找到符合条件的结果数，利用概率公式计算即可得结果．

    解：（1） ∵下午上第一节课的有3种等可能结果，
    ∴女老师抽到上第一节课的概率是 ；

    （2）画树状图为

    一共有6种等可能结果，其中女老师A比男老师B先上课的结果数为3，

    ∴P(女老师A比男老师B先上课)= .

    故答案为：（1） ；（2） .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

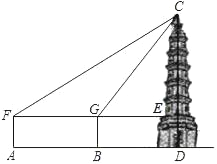
    【题目】计算：在一次数学社团活动课上，同学们测量一座古塔CD的高度，他们首先在A处安置测量器，测得塔顶C的仰角∠CFE＝30°，然后往塔的方向前进100米到达B处，此时测得塔顶C的仰角∠CGE＝60°，已知测量器高1.5米，请你根据以上数据计算出古塔CD的高度．（保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种蔬菜每千克售价（元）与销售月份之间的关系如图1所示，每千克成本（元）与销售月份之间的关系如图2所示，其中图1中的点在同一条线段上，图2中的点在同一条抛物线上，且抛物线的最低点的坐标为（6，1）．

    （1）求出与之间满足的函数表达式，并直接写出的取值范围；

    （2）求出与之间满足的函数表达式；

    （3）设这种蔬菜每千克收益为元，试问在哪个月份出售这种蔬菜，将取得最大值？并求出此最大值．（收益=售价-成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD是△ABC的角平分线，线段AD的垂直平分线分别交AB和AC于点E、F，连接DE、DF.

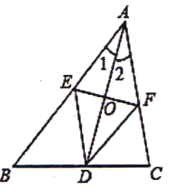
    （1）试判定四边形AEDF的形状，并证明你的结论.

    （2）若DE=13，EF=10，求AD的长.

    （3）△ABC满足什么条件时，四边形AEDF是正方形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】元旦期间，某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.

    （1）求甲、乙两种苹果的进价分别是每千克多少元？

    （2）在（1）的情况下，超市平均每天可售出甲种苹果100千克和乙种苹果140千克，若将这两种苹果的售价各提高1元，则超市每天这两种苹果均少售出10千克，超市决定把这两种苹果的售价提高x元，在不考虑其他因素的条件下，使超市销售这两种苹果共获利960元，求x的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

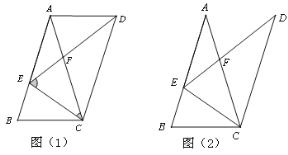
    【题目】在△ABC中，AB=AC，BC=2,将△ABC绕点C顺针方向旋转α（0°＜α＜360°），得到△DEC，使点E在AB边上。

    （1）如图1，连接AD，

    ①求证：四边形ABCD是平行四边形；

    ② 当AE=AD时，求旋转角α的度数；

    （2）如图2，若AE=2BE,求AB的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

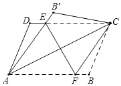
    【题目】如图，现将平行四边形ABCD沿其对角线AC折叠，使点B落在点B′处．AB′与CD交于点E．

    （1）求证：△AED≌△CEB′；

    （2）过点E作EF⊥AC交AB于点F，连接CF，判断四边形AECF的形状并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．

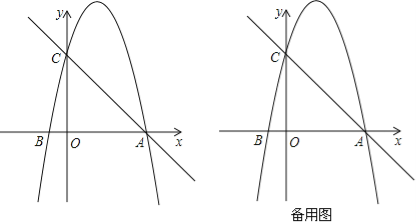
    （1）求抛物线的解析式；

    （2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

    （3）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=2，点E在边AD上，∠ABE=45°，BE=DE，连接BD，点P在线段DE上，过点P作PQ∥BD交BE于点Q，连接QD．设PD=x，△PQD的面积为y，则能表示y与x函数关系的图象大致是（　　）

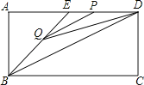
    查看答案和解析>>

    同步练习册答案