
【题目】在△ABC中,点A到直线BC的距离为d,AB>AC>d,以A为圆心,AC为半径画圆弧,圆弧交直线BC于点D,过点D作DE∥AC交直线AB于点E,若BC=4,DE=1,∠EDA=∠ACD,则AD=__________.
【答案】2或-2+2![]()
【解析】
当∠ACB为锐角时,根据题意易证∠BDE=∠ADE=∠ADC=∠ACD=60°,则△ACD为等边三角形,设AD=x,根据△BDE∽△BCA,列出关于x的方程,然后求解方程即可,同理求出当∠ACB为钝角时,AD的长即可.
解:如图,当∠C为锐角时,
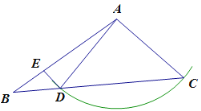
∵AD=AC,
∴∠ADC=∠ACD,
∵DE∥AC,
∴∠BDE=∠ACD,
已知∠EDA=∠ACD,
∴∠BDE=∠ADE=∠ADC=∠ACD=60°,
∴△ACD为等边三角形,
∵DE∥AC,
∴△BDE∽△BCA,
设AD=AC=CD=x,
则![]() ,即
,即![]() ,
,
解得x=2,
∴AD=2;
如图,当∠ACB为钝角时,
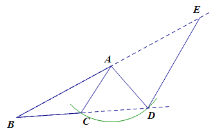
同理可得△ACD为等边三角形,
∵DE∥AC,
∴△BCA∽△BDE,
设AD=AC=CD=x,
则![]() ,即
,即![]() ,
,
解得x=﹣2+2![]() ,
,
∴AD=﹣2+2![]() .
.
故答案为:2或-2+2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
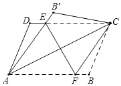
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
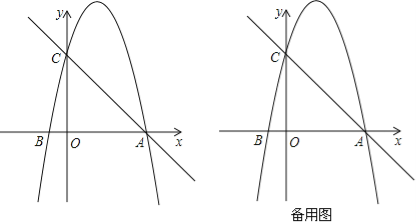
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
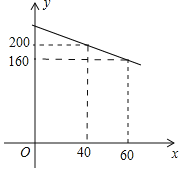
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
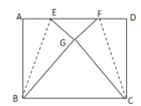
【题目】如图,在矩形ABCD中,2AB>BC,点E和点F为边AD上两点,将矩形沿着BE和CF折叠,点A和点D恰好重合于矩形内部的点G处,
(1)当AB=BC时,求∠GEF的度数;
(2)若AB=![]() ,BC=2,求EF的长.
,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
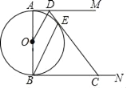
【题目】如图,⊙O的直径AB=6,AM,BN是⊙O的两条切线,点D是AM上一点,连接OD,作BE∥OD交⊙O于点E,连接DE并延长交BN于点.
(1)求证:DC是⊙O的切线;
(2)设AD=x,BC=y.求y与x的函数关系式(不要求写出自变量的取值范围)
(3)若AD=1,连接AE并延长交BC于F,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
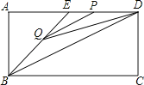
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
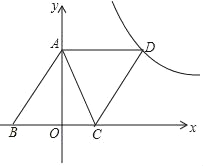
【题目】如图,直线y=﹣2x+4与x轴,y轴分别交于点C,A,点D为点B(﹣3,0)关于AC的对称点,反比例函数y=![]() 的图象经过点D.
的图象经过点D.
(1)求证:四边形ABCD为菱形;
(2)求反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求点M的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com