
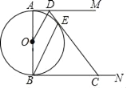
【题目】如图,⊙O的直径AB=6,AM,BN是⊙O的两条切线,点D是AM上一点,连接OD,作BE∥OD交⊙O于点E,连接DE并延长交BN于点.
(1)求证:DC是⊙O的切线;
(2)设AD=x,BC=y.求y与x的函数关系式(不要求写出自变量的取值范围)
(3)若AD=1,连接AE并延长交BC于F,求EF的长.
【答案】(1)见解析;(2)y=![]() ;(3)EF=
;(3)EF=![]() .
.
【解析】
(1)证明△OAD≌△OED(SAS),即可求解;
(2)利用OC2=(OBsinα+BCcosα)2=OB2+BC2,即可求解;
(3)在Rt△AOD中,tanα=![]() ,则cosα=
,则cosα=![]() ,在等腰三角形△EFC中,EF=2ECcosα,即可求解.
,在等腰三角形△EFC中,EF=2ECcosα,即可求解.
(1)连接OE,
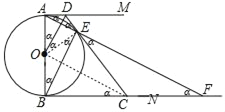
∵BE∥OD,∴∠AOD=∠ABE=∠OEB=∠DOE=∠α,
AO=OE,OD=OD,
∴△OAD≌△OED(SAS),
∴∠OED=∠OAD=90°,
∴DC是⊙O的切线;
(2)连接OC,
∵DC是⊙O的切线,
∴BE⊥OC,
∠OBE=∠OCB=α,
在Rt△AOD中,tanα=![]() ,则sinα=
,则sinα=![]() ,cosα=
,cosα=![]() ,
,
OC2=(OBsinα+BCcosα)2=OB2+BC2,
其中OB=3,BC=y,代入上式并整理得:y=![]() ;
;
(3)∵AM∥BN,
∴∠MAF=∠AFN=α,而∠DAE=∠DEA=α,
∴∠CEF=∠CFE=α,
由(2)知,当x=1时,y=9,
即:AD=AE=1,EC=CF=9,
在Rt△AOD中,tanα=![]() ,则cosα=
,则cosα=![]() ,
,
在等腰三角形△EFC中,
EF=2ECcosα=2×9×![]() =
=![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合.展开后,折痕
重合.展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .连接
.连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() .
.
其中正确结论的序号是( )
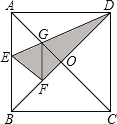
A. ①②③④⑤B. ①②③④C. ①③④⑤D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点A到直线BC的距离为d,AB>AC>d,以A为圆心,AC为半径画圆弧,圆弧交直线BC于点D,过点D作DE∥AC交直线AB于点E,若BC=4,DE=1,∠EDA=∠ACD,则AD=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,AD⊥BC,垂足为点D,以AD为对角线作正方形AEDF,DE交AB于点M,DF交AC于点N,连结EF,EF分别交AB、AD、AC于点G、点O、点H.
(1)求证:EG=HF;
(2)当∠BAC=60°时,求![]() 的值;
的值;
(3)设![]() ,△AEH和四边形EDNH的面积分别为S1和S2,求
,△AEH和四边形EDNH的面积分别为S1和S2,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y=![]() (x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,已知
中,已知![]() ,在边
,在边![]() 上取点
上取点![]() ,使
,使![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() ,与边
,与边![]() 或其延长线交于点
或其延长线交于点![]() .
.
猜想:如图①,当点![]() 在边
在边![]() 上时,线段
上时,线段![]() 与
与![]() 的大小关系为 .
的大小关系为 .
探究:如图②,当点![]() 在边
在边![]() 的延长线上时,
的延长线上时,![]() 与边
与边![]() 交于点
交于点![]() .判断线段
.判断线段![]() 与
与![]() 的大小关系,并加以证明.
的大小关系,并加以证明.
应用:如图②,若![]() 利用探究得到的结论,求线段
利用探究得到的结论,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价![]() (元)与产品日销售量
(元)与产品日销售量![]() (元)间的关系如下:
(元)间的关系如下:
| … | 12 | 15 | 18 | 21 | 24 | … |
| … | 28 | 25 | 22 | 19 | 16 | … |
日销售量![]() 是销售价
是销售价![]() 的一次函数.
的一次函数.
(1)求出日销售量![]() (件)与销售量
(件)与销售量![]() (元)的函数关系式.
(元)的函数关系式.
(2)要使每日的销售利润200元,每件产品的销售应定为多少元?进货成本多少元?
(3)选作:要使每日的销售的利润最大,每件产品的销售价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com