
【题目】在Rt△ABC中,∠B=60°,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为:___________.
【答案】![]()
【解析】
画出图形,由折叠的性质得出BD=B′D,由三角形的三条边的数量关系得AB′>AD-B′D,即AB′>AD-BD,推出△DBE沿DE折叠B点落在AD上时,AB′=AD-BD,此时A′B最小,由三角函数求出AC=BCtan60°=3![]() ,由勾股定理求出AD,即可得出结果.
,由勾股定理求出AD,即可得出结果.
如图所示:
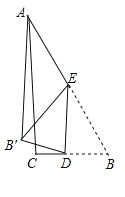
∵△DBE沿DE折叠到△DB′E,
∴BD=B′D,
∵在△AB′D中,AB′>AD-B′D,
∴AB′>AD-BD,
∴△DBE沿DE折叠B点落在AD上时,AB′=AD-BD,此时A′B最小,
∵在Rt△ABC中,∠B=60°,BC=3,
∴AC=BCtan60°=3![]() ,
,
∵BD=2CD,
∴CD=1,BD=2,
由勾股定理得:AD=![]() ,
,
∴A′B=AD-BD=![]() .
.
故答案是:![]()


科目:初中数学 来源: 题型:
【题目】如果a:b=b:c,即b2=ac,则b叫a和c的比例中项,或等比中项.若一个三角形一条边是另两条边的等比中项,我们把这个三角形叫做等比三角形.
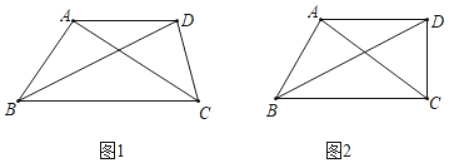
(1)已知△ABC是等比三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;
(2)如图,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC,求证:△ABC是等比三角形;
(3)如图2,在(2)的条件下,当∠ADC=90时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是![]()
![]()
A. 某种彩票的中奖机会是![]() 则买100张这种彩票一定会中奖
则买100张这种彩票一定会中奖
B. 为了解全国中学生的睡眠情况,应该采用普查的方式
C. 一组数据3,4,5,5,5,6,10的平均数大于中位数
D. 同时抛掷两枚均匀的硬币,出现一枚正面朝上且另一枚反面朝上的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为![]() 米,tanA=
米,tanA=![]() .现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
.现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
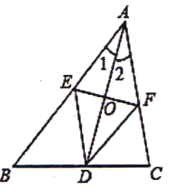
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若DE=13,EF=10,求AD的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
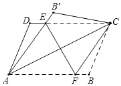
【题目】如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
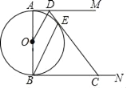
【题目】如图,⊙O的直径AB=6,AM,BN是⊙O的两条切线,点D是AM上一点,连接OD,作BE∥OD交⊙O于点E,连接DE并延长交BN于点.
(1)求证:DC是⊙O的切线;
(2)设AD=x,BC=y.求y与x的函数关系式(不要求写出自变量的取值范围)
(3)若AD=1,连接AE并延长交BC于F,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com