
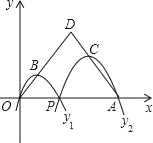
【题目】如图,已知点A(12,0),O为坐标原点,P是线段OA上任一点(不含端点O、A),二次函数y1的图象过P、O两点,二次函数y2的图象过P、A两点,它们的开口均向下,顶点分别为B、C,射线OB与射线AC相交于点D.则当OD=AD=9时,这两个二次函数的最大值之和等于( )
A. 8 B. 3![]() C. 2
C. 2![]() D. 6
D. 6
【答案】B
【解析】
过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,则BF+CM是这两个二次函数的最大值之和,BF∥DE∥CM,求出AE=OE=6,DE=3![]()
7 |
.设P(2x,0),根据二次函数的对称性得出OF=PF=x,推出△OBF∽△ODE,△ACM∽△ADE,得出![]() =
=![]() =
=![]()
![]() ,代入求出BF和CM,相加即可求出答案.
,代入求出BF和CM,相加即可求出答案.
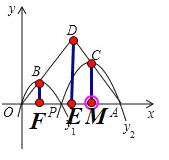
过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,
∵BF⊥OA,DE⊥OA,CM⊥OA,
∴BF∥DE∥CM,
∵OD=AD=9,DE⊥OA,
∴OE=EA=![]() OA=6,
OA=6,
由勾股定理得:DE=![]() =3
=3![]() ,
,
设P(2x,0),根据二次函数的对称性得出OF=PF=x,
∵BF∥DE∥CM,
∴△OBF∽△ODE,△ACM∽△ADE,
∴![]() =
=![]() =
=![]()
![]() ,
,
∵AM=PM=![]() (OA-OP)=
(OA-OP)=![]() (12-2x)=6-x,
(12-2x)=6-x,
即![]() =
=![]() ,
,![]() =
=![]() ,
,
解得:BF=![]() ,CM=
,CM=![]() ,
,
∴BF+CM=3![]()
故答案选B.


科目:初中数学 来源: 题型:
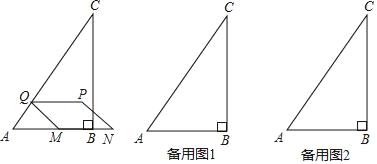
【题目】如图,已知在Rt△ABC中,∠ABC=90°,AB=6,BC=8,动点M以每秒2个单位的速度从点A出发,沿着A→B→C的方向运动,当点M到达点C时,运动停止.点N是点M关于点B的对称点,过点M作MQ⊥AC于点Q,以MN,MQ为边作MNPQ,设点M的运动时间为t秒.
(1)分别求当t=2和t=5时,线段MN的长;
(2)是否存在这样的t的值,使得MNPQ为菱形?若存在,请求出t的值;若不存在,请说明理由;
(3)作点P关于直线MQ的对称点P',当点P'落在△ABC内部时,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
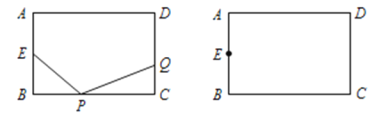
【题目】已知:如图,在长方形![]() 中,AB=4cm,BC=6cm,点
中,AB=4cm,BC=6cm,点![]() 为
为![]() 中点,如果点
中点,如果点![]() 在线段
在线段![]() 上以每秒2cm的速度由点
上以每秒2cm的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.设点
运动.设点![]() 运动时间为
运动时间为![]() 秒,若某一时刻△BPE与△CQP全等,求此时
秒,若某一时刻△BPE与△CQP全等,求此时![]() 的值及点
的值及点![]() 的运动速度.
的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
(1)若∠ACB=100°,求∠CAE的度数;
(2)若S△ABC=12,CD=4,求高AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
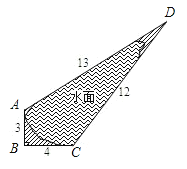
【题目】如图,某风景区的沿湖公路AB=3千米,BC=4千米,CD=12千米,AD=13千米,其中AB^BC,图中阴影是草地,其余是水面.那么乘游艇游点C出发,行进速度为每小时11![]() 千米,到达对岸AD最少要用 小时.
千米,到达对岸AD最少要用 小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
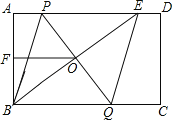
【题目】如图,在矩形ABCD中,E是AD边上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、QE
(1)求证:四边形BPEQ是菱形:
(2)若AB=6,F是AB中点,OF=4,求菱形BPEQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是
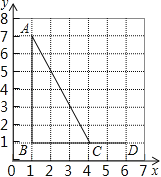
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com