
【题目】如图,某风景区的沿湖公路AB=3千米,BC=4千米,CD=12千米,AD=13千米,其中AB^BC,图中阴影是草地,其余是水面.那么乘游艇游点C出发,行进速度为每小时11![]() 千米,到达对岸AD最少要用 小时.
千米,到达对岸AD最少要用 小时.
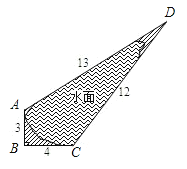
【答案】0.4
【解析】
连接AC,在直角△ABC中,已知AB,BC可以求AC,根据AC,CD,AD的长度符合勾股定理确定AC⊥CD,则可计算△ACD的面积,又因为△ACD的面积可以根据AD边和AD边上的高求得,故根据△ACD的面积可以求得C到AD的最短距离,即△ACD中AD边上的高.
解:连接AC,
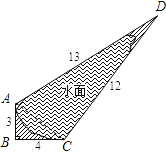
在直角△ABC中,AB=3km,BC=4km,则AC=![]() =5km,
=5km,
∵CD=12km,AD=13km,故存在AD2=AC2+CD2
∴△ACD为直角三角形,且∠ACD=90°,
∴△ACD的面积为![]() ×AC×CD=30km2,
×AC×CD=30km2,
∵AD=13km,∴AD边上的高,即C到AD的最短距离为![]() km,
km,
游艇的速度为11![]() km/小时,
km/小时,
需要时间为![]() 小时=0.4小时.
小时=0.4小时.
故答案为 0.4.


科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
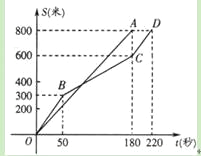
A、小莹的速度随时间的增大而增大B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇D、在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
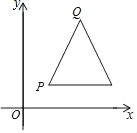
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若PQ为某个等腰三角形的腰,且该等腰三角形的底边与x轴平行,则称该等腰三角形为点P,Q的“相关等腰三角形”.下图为点P,Q的“相关等腰三角形”的示意图.
(1)已知点A的坐标为(0,1),点B的坐标为(-![]() ,0),则点A,B的“相关等腰三角形”的顶角为 °;
,0),则点A,B的“相关等腰三角形”的顶角为 °;
(2)若点C的坐标为(0,![]() ),点D在直线y=4
),点D在直线y=4![]() 上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
上,且C,D的“相关等腰三角形”为等边三角形,求直线CD的表达式;
(3)⊙O的半径为![]() ,点N在双曲线y=﹣
,点N在双曲线y=﹣![]() 上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
上.若在⊙O上存在一点M,使得点M、N的“相关等腰三角形”为直角三角形,直接写出点N的横坐标xN的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(12,0),O为坐标原点,P是线段OA上任一点(不含端点O、A),二次函数y1的图象过P、O两点,二次函数y2的图象过P、A两点,它们的开口均向下,顶点分别为B、C,射线OB与射线AC相交于点D.则当OD=AD=9时,这两个二次函数的最大值之和等于( )
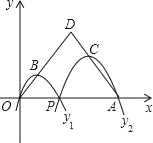
A. 8 B. 3![]() C. 2
C. 2![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明受《乌鸦喝水》故事的启发,利用量桶和体积相同的小球进行了如下操作:请根据图中给出的信息,解答下列问题:
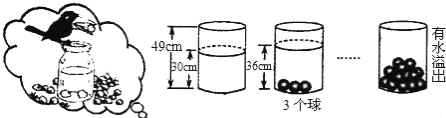
(1)放入一个小球量桶中水面升高 cm;
(2)求放入小球后量桶中水面的高度y(cm)与小球个数x(个)之间的函数关系式;
(3)当量桶中水面上升至距离量桶顶部3cm时,应在量桶中放入几个小球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形![]() 中,动点
中,动点![]() 从
从![]() 点出发,以每秒1个单位长度的速度沿
点出发,以每秒1个单位长度的速度沿![]() 向
向![]() 点运动,同时动点
点运动,同时动点![]() 从
从![]() 点出发,以每秒2个单位长度的速度沿
点出发,以每秒2个单位长度的速度沿![]() 方向运动,当
方向运动,当![]() 运动到
运动到![]() 点时,
点时,![]() 、
、![]() 两点同时停止运动.设
两点同时停止运动.设![]() 点运动的时间为
点运动的时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数关系的图象是( )
的函数关系的图象是( )

A.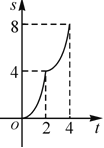 B.
B.
C.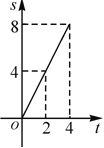 D.
D.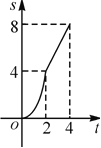
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,E是BC边上一点,将矩形沿AE折叠,点B落在点B'处,当△B'EC是直角三角形时,BE的长为( )
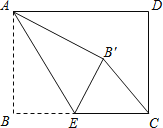
A.2B.6C.3或6D.2或3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
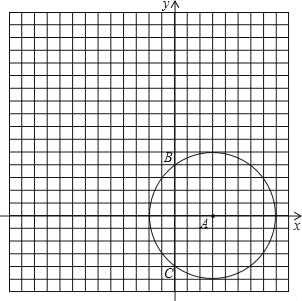
【题目】如图,正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系,圆心为 A(3,0)的⊙A被y轴截得的弦长BC=8.
解答下列问题:
(1)求⊙A 的半径;
(2)请在图中将⊙A 先向上平移 6 个单位,再向左平移8个单位得到⊙D,并写出圆心D的坐标;
(3)观察你所画的图形,对⊙D 与⊙A 的位置关系作出合情的猜想,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内有两点E、F满足AE=FC= 4,EF =6,AE⊥EF,CF⊥EF,则正方形ABCD的面积为 ( )
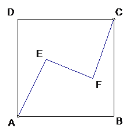
A.24B.25C.48D.50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com