
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OCDE�Ķ���C��E�ֱ���y����������x����������ϣ�OC=8��OE=17��������y=![]() x2��3x+m��y���ཻ�ڵ�A�������ߵĶԳ�����x���ཻ�ڵ�B����CD���ڵ�K��
x2��3x+m��y���ཻ�ڵ�A�������ߵĶԳ�����x���ཻ�ڵ�B����CD���ڵ�K��
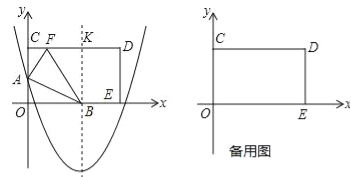
��1��������OCDE��AB�۵�����Oǡ�����ڱ�CD�ϵĵ�F����
����B�������� �� ����BK�ij��� ��CK�ij��� ��
�����F�����ꣻ
����ֱ��д�������ߵĺ�������ʽ��
��2��������OCDE���ž�����E��ֱ���۵�����Oǡ�����ڱ�CD�ϵĵ�G��������OG���ۺ���OG�ཻ�ڵ�H����M���߶�EH�ϵ�һ�����㣨�����H�غϣ�������MG��MO������G��GP��OM�ڵ�P����EH�ڵ�N������ON����M�ӵ�E��ʼ���߶�EH���H�˶��������N�غ�ʱֹͣ����MOG����NOG������ֱ��ʾΪS1��S2���ڵ�M���˶������У�S1S2����S1��S2�Ļ�����ֵ�Ƿ����仯�����仯����ֱ��д���仯��Χ�������䣬��ֱ��д�����ֵ��
��ܰ��ʾ���������Ը������⣬�ڱ���ͼ�в���ͼ�Σ��Ա�����
���𰸡���1����10��0��8��10������4��8������y=![]() x2��3x+5.��2�����䣮S1S2=189��
x2��3x+5.��2�����䣮S1S2=189��
�������������������1���������ı���OCKB�Ǿ����Լ��Գ��ṫʽ���ɽ�����⣮����RT��BKF�����ù��ɶ������ɽ�����⣮����OA=AF=x����RT��ACF�У�AC=8��x��AF=x��CF=4�����ù��ɶ������ɽ�����⣮
��2�����䣮S1S2=189������GHN�ס�MHG����![]() ���õ�GH2=HNHM�����GH2������S1S2=
���õ�GH2=HNHM�����GH2������S1S2=![]() OGHN
OGHN![]() OGHM���ɽ�����⣮
OGHM���ɽ�����⣮
�����������1����ͼ1�У��١�������y=![]() x2��3x+m�ĶԳ���x=��
x2��3x+m�ĶԳ���x=��![]() =10��
=10��
����B���꣨10��0����
���ı���OBKC�Ǿ��Σ�
��CK=OB=10��KB=OC=8��
�ʴ𰸷ֱ�Ϊ10��0��8��10��
����RT��FBK�У��ߡ�FKB=90����BF=OB=10��BK=OC=8��
��FK=![]() =6��
=6��
��CF=CK��FK=4��
����F���꣨4��8����
����OA=AF=x��
��RT��ACF����AC2+CF2=AF2��
����8��x��2+42=x2��
��x=5��
����A���꣨0��5��������������y=![]() x2��3x+m��m=5��
x2��3x+m��m=5��
��������Ϊy=![]() x2��3x+5��
x2��3x+5��
��2�����䣮S1S2=189��
���ɣ���ͼ2�У���RT��EDG�У���GE=EO=17��ED=8��
��DG=![]() =15��
=15��
��CG=CD��DG=2��
��OG=![]() =2
=2![]() ��
��
��CP��OM��MH��OG��
���NPN=��NHG=90����
�ߡ�HNG+��HGN=90������PNM+��PMN=90������HNG=��PNM��
���HGN=��NMP��
�ߡ�NMP=��HMG����GHN=��GHM��
���GHN�ס�MHG��
��![]() ��
��
��GH2=HNHM��
��GH=OH=![]() ��
��
��HNHM=17��
��S1S2=![]() OGHN
OGHN![]() OGHM=��
OGHM=��![]() 2
2![]() ��217=289��
��217=289��


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���װ��Ϊ�˽��װ�����������ͳ����ÿλӪҵԱ��ij�µ����۶��λ����Ԫ����������ͳ�Ƶ��������ݣ����Ƴ����µ�ͳ��ͼ�ٺ�ͼ�ڣ�����������Ϣ������������⣮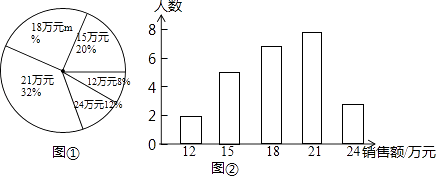
��1�����̳���װ��ӪҵԱ������Ϊ ��ͼ����m��ֵΪ .
��2����ͳ�Ƶ��������۶�����ݵ�ƽ��������������λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ѧϰ��Ʒ���վ�������������²���������ʶ�𣬸����±�������������⣺
��1��С�������Զ�Ǧ�ʡ��Ǻűʸ���֧��
��2����С���ٴι�����Ƥ�ʼDZ����Զ�Ǧ�������ľߣ�������15Ԫ�������ļ��ֲ�ͬ�Ĺ�����
��Ʒ�� | ���ۣ�Ԫ�� | ���������� | ��Ԫ�� |
ǩ�ֱ� | 3 | 2 | 6 |
�Զ�Ǧ�� | 1.5 | �� | �� |
�Ǻű� | 4 | �� | �� |
��Ƥ�ʼDZ� | �� | 2 | 9 |
Բ�� | 3.5 | 1 | �� |
�ϼ� | 8 | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������2[(m��1)m��m(m��1)]��[(m��1)m��m(m��1)]����m��������������۲컯���Ľ�����㷢��ԭʽ��ʾһ��ʲô����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��ʾ����֪��AOB��90������BOC��30����OMƽ�֡�AOC��ONƽ�֡�BOC�����MON�Ķ�����
(2)���(1)�С�AOB�����������������䣬���MON�Ķ�����
(3)���(1)�С�BOC����(��Ϊ���)�������������������MON�Ķ�����
(4)��(1)(2)(3)�Ľ�������ܿ���ʲô���ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У�����D��DE��AB�ڵ�E����F �ڱ�CD�ϣ�DF=BE������AF��BF�� 
��1����֤���ı���BFDE�Ǿ��Σ�
��2����CF=3��BF=4��DF=5����֤��AFƽ�֡�DAB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ں���y��kx��k��0����ͼ����������A1��x1��y1����A2��x2��y2����A3��x3��y3������֪x1��x2��0��x3�������и�ʽ����ȷ���ǣ� ��
A. y1��0��y3 B. y3��0��y1 C. y2��y1��y3 D. y3��y1��y2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com