
【题目】某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题.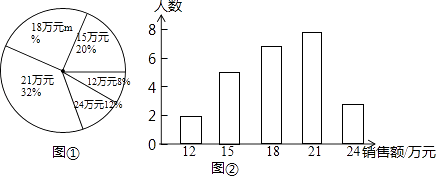
(1)该商场服装部营业员的人数为 ,图①中m的值为 .
(2)求统计的这组销售额额数据的平均数、众数和中位数.
科目:初中数学 来源: 题型:
【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
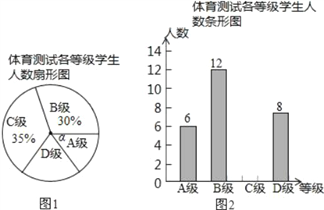
【题目】为了解中考体育科目训练情况,某区从九年级学生中抽取了部分学生进行了一次中考体育科测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 ,并把图2条形统计图补充完整;
(3)该区九年级有学生4000名,如果全部参加这次体育测试,请估计不及格的人数为 ;
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树状图的方法求出选中小明的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 到
到![]() 两边的距离相等,且
两边的距离相等,且![]() .
.
(1)先用尺规作出符合要求的点![]() (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设![]() ,
,![]() ,试用
,试用![]() 、
、![]() 的代数式表示
的代数式表示![]() 的周长和面积;
的周长和面积;
(3)设![]() 与
与![]() 交于点
交于点![]() ,试探索当边
,试探索当边![]() 、
、![]() 的长度变化时,
的长度变化时,![]() 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“割圆术”是求圆周率的一种算法,公元263年左右,我国一位著名的数学家发现当圆的内接正多边形的边数无限增加时,多边形面积可无限逼近圆面积,即所谓“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”. 请问上述著名数学家为 ( )
A.刘徽B.祖冲之C.杨辉D.赵爽
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
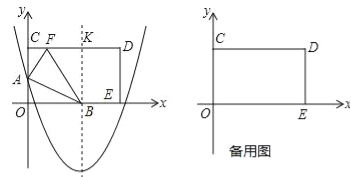
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com