
【题目】根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点A(0,-1),B(1,0),C(-1,2);
(2)已知抛物线的顶点为(1,-3),且与y轴交于点(0,1);
(3)已知抛物线与x轴交于点M(-3,0),(5,0),且与y轴交于点(0,-3);
(4)已知抛物线的顶点为(3,-2),且与x轴两交点间的距离为4.
【答案】(1)![]()
(2)![]()
(3)![]()
(4)![]()
【解析】
试题分析:
(1)已知三点坐标,所以设解析式为![]() ,列三元一次方程组求解即可.
,列三元一次方程组求解即可.
(2)已知顶点为(1,-3),所以设解析式为![]() ,把点(0,1)坐标代入即可求得.
,把点(0,1)坐标代入即可求得.
(3)根据抛物线与x轴的两个交点的坐标,可设函数解析式为![]() ,再根据抛物线与y轴的交点可求出a的值;
,再根据抛物线与y轴的交点可求出a的值;
(4)根据已知抛物线的顶点坐标(3,-2),可设函数解析式为![]() ,同时可知抛物线的对称轴为x=3,再由与x轴两交点间的距离为4,可得抛物线与x轴的两个交点为(1,0)和(5,0),任选一个代入关系式为
,同时可知抛物线的对称轴为x=3,再由与x轴两交点间的距离为4,可得抛物线与x轴的两个交点为(1,0)和(5,0),任选一个代入关系式为![]() ,即可求出a的值.
,即可求出a的值.
试题解析:
解:(1)设二次函数的解析式为:![]() ,
,
依题意得:
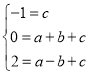 解得:
解得: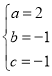
∴![]()
(2)∵图象的顶点为(1,-3),
∴设其解析式为![]() ,
,
∵经过点(0,1)
∴![]() ,解得a=4,
,解得a=4,
∴![]()
(3)∵抛物线与x轴交于点M(-3,0).(5,0),
∴设二此函数的解析式为![]() ,
,
又∵抛物线与y轴交于点(0,-3),可以得到![]() ,解得
,解得![]() .
.
∴所求二次函数的解析式为![]() .
.
即![]()
(4)因为顶点坐标(3,-2),所以可设函数解析式为![]() ,
,
并且抛物线的对称轴为x=3,
由与x轴两交点间的距离为4,可得抛物线与x轴的两个交点为(1,0)和(5,0),
把(1,0)代入关系式为![]() ,得
,得
![]()
解得![]() .
.
所以![]()


科目:初中数学 来源: 题型:
【题目】我县某初中七年级进行了一次数学测验,参加人数共540人,为了了解这次数学测验成绩,下列所抽取的样本中较为合理的是( )
A.抽取前100名同学的数学成绩
B.抽取后100名同学的数学成绩
C.抽取(1)(2)两班同学的数学成绩
D.抽取各班学号为6号的倍数的同学的数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是确定事件的是( )
A. 打开电视机,它正在播放广告
B. 明天一定是天晴
C. 任意掷一枚质地均匀的骰子,掷出的点数是奇数
D. 抛出的篮球会下落
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形的一个内角平分线把矩形的一条边分成3cm和5cm两部分,则矩形的周长( )
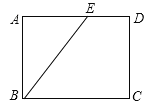
A.16cm B.22cm和16cm C.26cm D.22cm和26cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com