

分析 (1)先根据OB平分∠COD得出∠BOC及∠AOC的度数,进而可得出结论;
(2)根据直角三角板的性质得出∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°进而可得出结论;
(3)根据(1)、(2)的结论可知∠AOD+∠BOC=180°,故可得出∠AOD=180°-∠BOC,根据∠BOC的余角的4倍等于∠AOD即可得出结论.
解答 解:(1)∵OB平分∠COD,
∴∠BOC=∠BOD=45°.
∵∠AOC+∠BOC=45°,
∴∠AOC=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°.
故答案为:180°;
(2)∵∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=90°+90°=180°;
(3)∵由(1)、(2)得,∠AOD+∠BOC=180°,
∴∠AOD=180°-∠BOC.
∵∠AOD=4(90°-∠BOC),
∴180°-∠BOC=4(90°-∠BOC),
∴∠BOC=60°.
点评 本题考查的是余角和补角及角平分线的定义,熟知直角三角板的特点是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
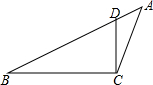 如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )
如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD•AB;④AB•CD=AD•CB,能满足△ADC与△ACB相似的条件是( )| A. | ①、②、③ | B. | ①、③、④ | C. | ②、③、④ | D. | ①、②、④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=AC,点D为AC上一点,且BD=BC.将△BCD沿直线BD折叠后,点C落在AB上的点E处,若AE=DE,则∠A的度数为36°.
如图,△ABC中,AB=AC,点D为AC上一点,且BD=BC.将△BCD沿直线BD折叠后,点C落在AB上的点E处,若AE=DE,则∠A的度数为36°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
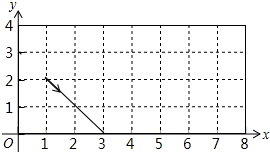 如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )
如图,动点P从(1,2)出发,沿图中箭头所示方向运动,每当碰到长方形的边时反弹(反弹时反射角等于入射角),假设反弹可以无限进行下去,则在点P运动路径上的点是( )| A. | (0,5) | B. | (5,0) | C. | (3,3) | D. | (7,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com