
 如图,PA、PB是⊙O的切线,切点分别为A、B,∠APB=60°,⊙O的半径为2cm,则
如图,PA、PB是⊙O的切线,切点分别为A、B,∠APB=60°,⊙O的半径为2cm,则分析 (1)根据切线长定理、以及切线的性质即可解决问题.
(2)在Rt△PAO中,根据39度角性质,可得OP=2OA,再根据勾股定理即可解决问题.
(3)只要证明△PAB是等边三角形即可解决问题.
解答  解:(1)∵PA、PB是⊙O的切线,切点分别为A、B,∠APB=60°,
解:(1)∵PA、PB是⊙O的切线,切点分别为A、B,∠APB=60°,
∴PA=PB,∠OPA=∠OPB=30°,OB⊥PB,
∴∠PBO=90°,∠BOP=90°-∠OPB=60°,
故答案分别为30,60.
(2)∵PA是⊙O切线,
∴OA⊥PA,
∴∠OAP=90°,
∵AO=2,∠APO=30°,
∴PO=2OA=4,PA=PB=$\sqrt{O{P}^{2}-O{A}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
故答案分别为4,2$\sqrt{3}$,2$\sqrt{3}$.
(3)∵PA=PB,∠APB=60°,
∴△PAB是等边三角形,
∴△PAB的周长为6$\sqrt{3}$.
故答案为6$\sqrt{3}$.
点评 本题考查切线的性质、切线长定理、直角三角形30度角性质、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,属于基础题,中考常考题型.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | -ma-m=-m(a-1) | B. | a2-1=(a-1)2 | C. | a2-6a+9=(a-3)2 | D. | a2+3a+9=(a+3)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
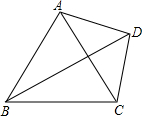 己知:如图,四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,且∠BAD+∠CAD=180°,那么∠BDC的度数为29°.
己知:如图,四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,且∠BAD+∠CAD=180°,那么∠BDC的度数为29°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
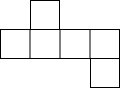 现有一张长为30cm,宽为20cm的长方形材料,若将其裁剪出一个如图所示的正方体表面展开图,要求使折叠后的正方体表面积最大,且正方体的棱长为整数,那么余料的面积是384cm2.
现有一张长为30cm,宽为20cm的长方形材料,若将其裁剪出一个如图所示的正方体表面展开图,要求使折叠后的正方体表面积最大,且正方体的棱长为整数,那么余料的面积是384cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
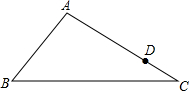 如图,在△ABC中,AB=3,BC=8,AC=6,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是24.
如图,在△ABC中,AB=3,BC=8,AC=6,点D在边AC上,且CD=4,过点D作一条直线交边AB于点E,使△ADE与△ABC相似,则DE的长是24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com