练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．若正三角形的边心距为$\sqrt{3}$，则该正三角形半径为2$\sqrt{3}$；周长为18；面积为9$\sqrt{3}$．

    分析 如图，O是等边三角形△ABC的中心，OE⊥BC．在Rt△OEC中，解三角形即可解决问题．

    解答 解：如图，O是等边三角形△ABC的中心，OE⊥BC．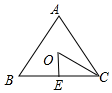

    在Rt△OEC中，∵∠OEC=90°，OE=$\sqrt{3}$，∠OCE=30°，
    ∴OC=2OE=2$\sqrt{3}$，EC=$\sqrt{3}$OE=3，BC=2EC=6，
    ∴△ABC的周长为18，
    ∴S△ABC=6•S△OEC=6×$\frac{1}{2}$×3×$\sqrt{3}$=9$\sqrt{3}$．
    故答案分别为2$\sqrt{3}$，18，9$\sqrt{3}$．

    点评 本题考查等边三角形的边心距、半径、周长、面积等知识，解题的关键是记住中心概念以及公式，属于基础题中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．一元二次方程2x2-1=6x的一般形式是2x2-6x-1=0，其中一次项系数是-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若圆内接正方形的边心距为2，则这个圆内接三角形的边长为2$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

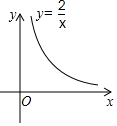    11．已知点A（1，y1），B（2，y2）是如图所示的反比例函数y=$\frac{2}{x}$图象上两点，则y1＞y2（填“＞”，“＜”或“=”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，PA、PB是⊙O的切线，切点分别为A、B，∠APB=60°，⊙O的半径为2cm，则
    （1）∠APO=30°，∠BOP=60°
    （2）OP=4cm，AP=2$\sqrt{3}$cm，BP=2$\sqrt{3}$cm．
    （3）△ABP的周长=6$\sqrt{3}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知点C是线段AB的黄金分割点，若$\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$，则$\frac{CB}{AC}$=$\frac{\sqrt{5}-1}{2}$，$\frac{CB}{AB}$=$\frac{3-\sqrt{5}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．a2-2ab-b2-（-3a2+ab-2b2）=-2a2-ab-3b2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知m＜0，化简2n$\sqrt{\frac{m}{n}}$+2m$\sqrt{\frac{n}{m}}$=-4$\sqrt{mn}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

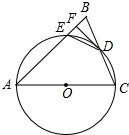    19．如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE．
    （1）求证：直线DF与⊙O相切；
    （2）若AE=7，BC=6，求BE的长．

    查看答案和解析>>

    同步练习册答案