
【题目】某学校准备印制一-批证书,现有两个印刷厂可供选择:
甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本时,超过的部分每本收印刷费0.25元,若该校印刷证书![]() 本.
本.
(1)若![]() 不超过2000时,甲厂的收费为 元,乙厂的收费为 元;
不超过2000时,甲厂的收费为 元,乙厂的收费为 元;
(2)若![]() 超过2000时,甲厂的收费为 元, 乙厂的收费为 元;
超过2000时,甲厂的收费为 元, 乙厂的收费为 元;
(3)当印制证书8000本时应该选择哪个印刷厂更节省费用?节省多少?
【答案】(1)1000+0.5x,1.5x;(2)1000+0.5x,2500+0.25x;(3)乙印刷厂省,省500元.
【解析】
(1)根据印刷费用=数量×单价可分别求得;
(2)根据甲厂印刷费用=数量×单价、乙厂印刷费用=2000×1.5+超出部分的费用可得;
(3)分别计算出x=8000时,甲、乙两厂的费用即可得.
(1)若x 不超过2000时,甲厂的收费为(1000+0.5x)元,乙厂的收费为(1.5x)元,
故答案为:1000+0.5x,1.5x;
(2)若x 超过2000时,甲厂的收费为(1000+0.5x)元,乙厂的收费为2000×1.5+0.25(x-2000)=0.25x+2500元,
故答案为:1000+0.5x,2500+0.25x;
(3)当x=8000时,甲厂费用为1000+0.5×8000=5000元,
乙厂费用为:0.25×8000+2500=4500元,
∴当印制证书8000本时应该选择乙印刷厂更节省费用,节省了500元.


科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A. 2 B. 2或![]() C.
C. ![]() 或
或![]() D. 2或
D. 2或![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在BC边所在直线上, PE=PB.
(1)如图1,当点E在线段BC上时,
求证:①PE=PD,②PE⊥PD.
简析: 由正方形的性质,图1中有三对全等的三角形,
即△ABC≌△ADC,_______≌_______,和_______≌______,由全等三角形性质,结合条件中PE=PB,易证PE=PD.要证PE⊥PD,考虑到∠ECD = 90°,故在四边形PECD中,只需证∠PDC +∠PEC=______即可.再结合全等三角形和等腰三角形PBE的性质,结论可证.

(2)如图2,当点E在线段BC的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;

(3)若AB=1,当△PBE是等边三角形时,请直接写出PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,数轴上
,数轴上![]() 两点所对应的数分别是
两点所对应的数分别是![]() 和
和![]() .
.
(1)填空:![]() ,
,![]() ;
;
(2)数轴上是否存在点![]() ,
,![]() 点在
点在![]() 点的右侧,且点
点的右侧,且点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点的距离的2倍?若存在,请求出点
点的距离的2倍?若存在,请求出点![]() 表示的数;若不存在,请说明理由;
表示的数;若不存在,请说明理由;
(3)点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 点出发向左运动,同时点
点出发向左运动,同时点![]() 以每秒3个单位的速度从
以每秒3个单位的速度从![]() 点出发向右运动,点
点出发向右运动,点![]() 以每秒4个单位的速度从原点
以每秒4个单位的速度从原点![]() 点出发向左运动.若
点出发向左运动.若![]() 为
为![]() 的中点,当
的中点,当![]() 时,求
时,求![]() 两点之间的距离.
两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH与BE相交于点G.

(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)CE与BG的大小关系如何?试证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为_______.
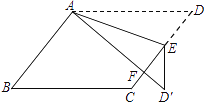
A. 36° B. 52° C. 48° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把ΔABC剪成三部分,边AB,BC,AC放在同一直线上,点O都落在直线MN上,直线MN∥AB.在ΔABC中,若∠AOB=125°,则∠ACB的度数为( )

A. 70°B. 65°C. 60°D. 85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为![]() ,则AK= .
,则AK= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com