
【题目】已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证: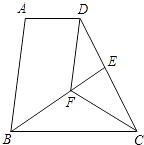
(1)△BFC≌△DFC;
(2)AD=DE.
【答案】
(1)证明:∵CF平分∠BCD,
∴∠BCF=∠DCF.
在△BFC和△DFC中,

∴△BFC≌△DFC(SAS)
(2)证明:连接BD. 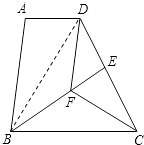
∵△BFC≌△DFC,
∴BF=DF,∴∠FBD=∠FDB.
∵DF∥AB,
∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,
∴∠BDA=∠DBC.
∵BC=DC,
∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
又∵BD是公共边,
∴△BAD≌△BED(ASA).
∴AD=DE.
【解析】(1)根据题意和SAS得得得△BFC≌△DFC;(2)由(1)知△BFC≌△DFC,根据对应边相等,得到BF=DF,再根据等腰三角形的性质得到∠FBD=∠FDB,由已知DF∥AB,再由ASA得到△BAD≌△BED,根据全等三角形的对应边相等,得到AD=DE.


科目:初中数学 来源: 题型:
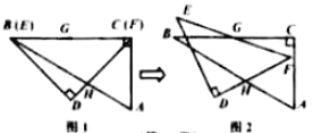
【题目】一副含![]() 和
和![]() 的三角板
的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,现将三角板
,现将三角板![]() 绕点
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,观察点
的变化过程中,观察点![]() 的位置变化,点
的位置变化,点![]() 相应移动的路径长为 (结果保留根号).
相应移动的路径长为 (结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
(1)如图1,若AB=![]() ,BE=5,求AE的长;
,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种商品按进货价提高100%后,又以6折优惠售出,售价为60元,则这种商品的进货价是( )
A.120元
B.100元
C.72元
D.50元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在y轴正半轴上,点B与点C都在x轴上,且点B在点C的左侧,满足BC=OA.若﹣3am﹣1b2与anb2n﹣2是同类项且OA=m,OB=n,求出m和n的值以及点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定两个直角三角形全等的是( )
A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与y轴交于点C(0,-1).且对称轴为
轴交于A、B两点,与y轴交于点C(0,-1).且对称轴为![]() .
.

(1)求抛物线的解析式及A、B两点的坐标;
(2)点D在x轴下方的抛物线上,则四边形ABDC的面积是否存在最大值,若存在,求出此时点D的坐标;若不存在,请说明理由;
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求出所有满足条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com