
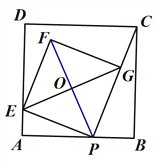
【题目】如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上. 对角线EG、FP相交于点O.
(1)若AP=3,求AE的长;
(2)连接AC,判断点O是否在AC上,并说明理由;
(3)在点P从点A到点B的运动过程中,正方形PEFG也随之运动,求DE的最小值.
【答案】(1)AE=![]() ;(2)见解析;(3)DE的最小值为3.
;(2)见解析;(3)DE的最小值为3.
【解析】试题分析:
(1)由已知易证∠A=∠B=∠EPG=90°,由此可得∠AEP+∠APE=90°,∠BPC+∠APE=90°,从而可得∠AEP=∠BPC,这样可证得△APE∽△BCP,再由相似三角形的性质结合AB=BC=4,AP=3即可求得AE的长;
(2)过点O分别作AB、AD的垂线,垂足分别为M、N,由已知条件易证△OPM≌△OEN,可得OM=ON,由此可得点O在∠BAD的平分线上,由正方形的对角线平分一组对角可得AC是∠BAD的平分线,从而说明点O在AC上;
(3)设AP=x,则BP=4﹣x,由(1)可知:△APE∽△BCP,从而可得![]() ,即
,即![]() ,解得:AE=x﹣
,解得:AE=x﹣![]() x2=﹣
x2=﹣![]() (x﹣2)2+1,结合AE+DE=AD=4可得DE=
(x﹣2)2+1,结合AE+DE=AD=4可得DE=![]() (x﹣2)2+3,由此即可得到DE的最小值为3.
(x﹣2)2+3,由此即可得到DE的最小值为3.
试题解析:
(1)∵四边形ABCD、四边形PEFG是正方形,
∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,
∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,
∴∠AEP=∠BPC,
∴△APE∽△BCP,
∴![]() ,即
,即![]() ,
,
解得:AE=![]() ;
;
(2)点O在AC上,理由:过点O分别作AD、AB的垂线,垂足分别为M、N,证得OM=ON,证得点O在∠BAD的平分线上,证得AC是∠BAD的平分线,所以,点O在AC上。

(3)设AP=x,则BP=4﹣x,由(1)可知:△APE∽△BCP,
∴![]() ,即
,即![]() ,
,
解得:AE=x﹣![]() x2=﹣
x2=﹣![]() (x﹣2)2+1,
(x﹣2)2+1,
∵AE+DE=AD=4,
∴DE=![]() (x﹣2)2+3,
(x﹣2)2+3,
∴DE的最小值为3.


科目:初中数学 来源: 题型:
【题目】我国古代对于利用方程解决实际问题早有研究,《九章算术》中提到这么一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺:若将绳四折测之,绳多一尺.绳长、井深各几何?
这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺:如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设井深为x尺,则求解井深的方程正确的是( )
A.3(x+4)=4(x+1)B.3x+4=4x+1
C.![]() x+4=
x+4=![]() x+1D.
x+1D.![]() x﹣4=
x﹣4=![]() x﹣1
x﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】低碳生活备受关注.小明为了了解人们到某超市购物时使用购物袋的情况,利用星期日到该超市对部分购物者进行调查,并把调查结果绘制成两幅不完整的统计图.假设当天每人每次购物时都只用一个环保购物袋(可降解)或塑料购物袋(不可降解).

A.一自备环保购物袋
B.一自备塑料购物袋
C.一购买环保购物袋
D.一购买塑料购物袋
根据以上信息,回答下列问题:
(1)小明这次调查到的购物人数是 人次;
(2)补全两幅统计图;
(3)若当天到该超市购物者共有2000人次,请你估计该天使用环保购物袋有 人次,使用塑料购物袋有 人次;
(4)在大力倡导低碳生活的今天,你认为在购物时应尽量使用 购物袋.(填“环保”或“塑料”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)图中的t1= 分;
(2)若乙提速后,乙登山的速度是甲登山的速度的3倍,
①则甲登山的速度是 米/分,图中的t2= 分;
②请求出乙登山过程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,tan∠ABC=![]() ,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则
,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,百年书院-----“安阳书院”近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明一个抽中“唐诗”一个抽中“宋词”的概率是多少? (请用“画树状图”或“列表”等方法写出分析过程)
(2)九年级一班班委会有2名男生和若干名女生,班级准备选派2名班委会成员参加学校举办的诗词比赛,若选派一名男生和一名女生的概率为![]() ,则班委会女生有 人.
,则班委会女生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com