
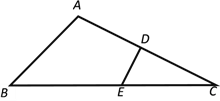
【题目】如图,已知△ABC中,∠B=45°,![]() ,BC=6.
,BC=6.
(1)求△ABC面积;
(2)AC的垂直平分线交AC于点D,交BC于点E. 求DE的长.
【答案】(1)6;(2) ![]()
【解析】分析:(1)过点A作AH⊥BC于点H,根据题意得到三角形ACH为等腰直角三角形,设AH=BH=x,根据tanC的值,表示出HC,由BC=6求出x的值,确定出AH的长,即可求出三角形ABC面积;
(2)由(1)得到AH与CH的长,利用勾股定理求出AC的长,进而确定出CD的长,根据tanC的值,利用锐角三角函数定义求出DE的长即可.
详解:(1)过点A作AH⊥BC于点H.在Rt△ABC中,∠B=45°,设AH=x,则BH=x.在Rt△AHC中,tanC=![]() =
=![]() ,∴HC=2x.∵BC=6,∴x+2x=6,解得:x=2,∴AH=2,∴S△ABC=
,∴HC=2x.∵BC=6,∴x+2x=6,解得:x=2,∴AH=2,∴S△ABC=![]() BCAH=6;
BCAH=6;
(2)由(1)得AH=2,CH=4.在Rt△AHC中,AC=![]() =2
=2![]() .∵DE垂直平分AC,∴CD=
.∵DE垂直平分AC,∴CD=![]() AC=
AC=![]() .∵ED⊥AC,∴在Rt△EDC中,tanC=
.∵ED⊥AC,∴在Rt△EDC中,tanC=![]() =
=![]() ,∴DE=
,∴DE=![]() .
.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】“我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为________________平方千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
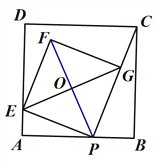
【题目】如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上. 对角线EG、FP相交于点O.
(1)若AP=3,求AE的长;
(2)连接AC,判断点O是否在AC上,并说明理由;
(3)在点P从点A到点B的运动过程中,正方形PEFG也随之运动,求DE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
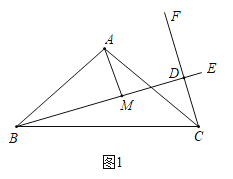
【题目】已知△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
⑴如图1所示,若BE⊥CF,AB=6,∠ABE=30°,求CD;
⑵如图2所示,求证:BM=DM﹣DC.
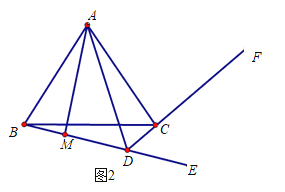
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的括号内:
+5,+![]() ,0.31,0,-1.3,
,0.31,0,-1.3,![]() ,62.6,-8.3,
,62.6,-8.3,![]() ,7,100
,7,100
(1)正整数:( )
(2)分数:( )
(3)非负数:( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,![]()
![]() ……,都是斜边在
……,都是斜边在![]() 轴上,斜边长分别为2,4,6……的等腰直角三角形,若
轴上,斜边长分别为2,4,6……的等腰直角三角形,若![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,则依图中所示规律,
,则依图中所示规律,![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A、D表示的数互为相反数,那么点B表示的数是多少?
(2)当点B为原点时,若存在一点M到A点的距离是点M到D点的距离的2倍,则点M所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,且OA=OB
(1)求证:四边形ABCD是矩形;
(2)若AB=5,∠AOB=60°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com