
����Ŀ����ͼ![]() ���߳���Ϊ
���߳���Ϊ![]() ����
����![]() ����
����![]() ԭ����ȫ�غϣ���ͼ
ԭ����ȫ�غϣ���ͼ![]() ���ֱ�����
���ֱ�����![]() ������ʹ��
������ʹ��![]() �������������εĹ������ĵ�
�������������εĹ������ĵ�![]() ��˳ʱ�뷽����ת������ת�Ƕ�Ϊ
��˳ʱ�뷽����ת������ת�Ƕ�Ϊ![]() ����ע������
����ע������![]() ���еĵڢ��ʣ��������ֻҪֱ�Ӹ���������ɣ�
���еĵڢ��ʣ��������ֻҪֱ�Ӹ���������ɣ�
![]() ��
��![]() ����ʱ����
����ʱ����![]() ����
����![]() ������ת�����еĵ�һ����ȫ�غϣ�
������ת�����еĵ�һ����ȫ�غϣ�
![]() ��
��![]() ʱ��Ҫʹ��
ʱ��Ҫʹ��![]() ����
����![]() �ص����������С��
�ص����������С��![]() ����ȡ��Щ�Ƕȣ�
����ȡ��Щ�Ƕȣ�
![]() ��תʱ����ͼ
��תʱ����ͼ![]() ����
����![]() ����
����![]() ʼ�վ��й��������Բ
ʼ�վ��й��������Բ![]() ����
����![]() ʱ������
ʱ������![]() ����
����![]() �ص�����Ϊ������
�ص�����Ϊ������![]() ����
����![]() �������Χ�ڱ仯ʱ��
�������Χ�ڱ仯ʱ��
����![]() ���
���![]() ��Ӧ�ı仯��Χ��
��Ӧ�ı仯��Χ��
��![]() ���ܳ��Ƿ�һ����˵��������ɣ�
���ܳ��Ƿ�һ����˵��������ɣ�

���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ʱ�ص����������С��
ʱ�ص����������С��![]() ��
��![]() ����
����![]() ���ܳ�һ�������ɼ�����.
���ܳ�һ�������ɼ�����.
��������
��1����Ϊ��B����A�غ�ʱ����A'B'C'������ABC������ת�����еĵ�һ����ȫ�غϣ�����=120�㣻
��2������A��B��C��������һ��������ABCƽ��ʱ�ص����������С���ɣ�1����֪��B����A�غ�ʱ����A'B'C'������ABC������ת�����еĵ�һ����ȫ�غ�ʱ��=60�������Ե���=60�㡢180����300��ʱ�ص����������С��
��3���������������εı߳���Ϊ6�����Ե�A��B����BCʱ����ADIΪ�ȱ������Σ�����ID=2������S��ADI=![]() IDAIsin60��=
IDAIsin60��=![]() ��2��2��
��2��2��![]() =
=![]() �������ɵó����ۣ�
�������ɵó����ۣ�
������AB��������AB=A'B'���ɵó�![]() ���ٸ���Բ�ܽǶ������ɵó�IA=IB'��DA=DA'�������ɵó����ۣ�
���ٸ���Բ�ܽǶ������ɵó�IA=IB'��DA=DA'�������ɵó����ۣ�
![]() �ߵ�
�ߵ�![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() ����
����![]() ������ת�����еĵ�һ����ȫ�غϣ���ʱ��
������ת�����еĵ�һ����ȫ�غϣ���ʱ��![]() ��
��![]() �غϣ���ת�Ƕ�
�غϣ���ת�Ƕ�![]() ��
��
�൱![]() ʱ����
ʱ����![]() ����
����![]()
������ת�����еĵ�һ����ȫ�غϣ�
![]() ��
��![]() ������һ������
������һ������![]() ƽ��ʱ�ص����������С��
ƽ��ʱ�ص����������С��
����![]() ��֪��
��֪��![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() ����
����![]() ������ת�����еĵ�һ����ȫ�غ�ʱ
������ת�����еĵ�һ����ȫ�غ�ʱ![]() ��
��
�൱![]() ��
��![]() ��
��![]() ʱ�ص����������С��
ʱ�ص����������С��
![]() �١��������εı߳���Ϊ
�١��������εı߳���Ϊ![]() ��
��
�൱![]() ʱ��
ʱ��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]() ���
���![]() ��Ӧ�ı仯��ΧΪ��
��Ӧ�ı仯��ΧΪ��![]()
��![]() ���ܳ�һ�����������£�
���ܳ�һ�����������£�
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
ͬ����![]() ��
��
��![]() ���ܳ���
���ܳ���![]() ��
��


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ������ö�ʵؾ��ȵ����ӣ����ӵ�������ֱ����1��6�ĵ��������ϵ���ĵ����У�һ�������ܱ���һ�����������ĸ����ǡ�
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=CB����ABC=90����DΪAB�ӳ�����һ�㣬��E��BC���ϣ���BE=BD������AE��DE��DC��

��1����֤����ABE�ա�CBD��
��2������CAE=30�������BCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڽ��ڡ�O����ABΪ��O��ֱ��OD��AB����AC���ڵ�E�������C�ġ�O���߽��ڵ�D��
��1����AC=6��BC=3����OE�ij���
��2�����жϡ�A���CDE��������ϵ����˵�����ɣ�
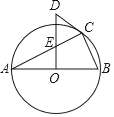
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��![]() �У�
��![]() ��
��![]() ��
��![]() ������һ�뾶Ϊ
������һ�뾶Ϊ![]() ��Բ�ֱ���
��Բ�ֱ���![]() ��
��![]() ���У������к��ַ������ҵ���Բ��Բ���� ��
���У������к��ַ������ҵ���Բ��Բ���� ��

A. ![]() �Ľ�ƽ������
�Ľ�ƽ������![]() �Ľ���
�Ľ���
B. ![]() �������
���д�����![]() �д��ߵĽ���
�д��ߵĽ���
C. ![]() �Ľ�ƽ������
�Ľ�ƽ������![]() �д��ߵĽ���
�д��ߵĽ���
D. ![]() �Ľ�ƽ������
�Ľ�ƽ������![]() �д��ߵĽ���
�д��ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����걾���۽۴������ijˮ��������һ���۽����ɱ���Ϊ10Ԫ/ǧ������֪���ۼ۲����ڳɱ���������۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ�����г����鷢�����ò�Ʒÿ���������y��ǧ���������ۼ�x��Ԫ/ǧ����֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ��
��2���þ�������Ҫÿ����150Ԫ���������������ۼ�Ӧ��Ϊ������
����������=���ۼ����ɱ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC����ACB��ƽ���߽��ڵ�O������A=40�������BOC�Ķ���Ϊ�� ��

A.40��B.80��C.100��D.110��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У���
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ����
�ϣ����![]() ����
����![]() ����ô����˵���У�������ǣ� ��
����ô����˵���У�������ǣ� ��

A. ��ADE�ס�ABC B. ��ADE�ס�ACD
C. ��ADE�ס�DCB D. ��DEC�ס�CDB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=x2+bx+c����A����4����3������y�ύ�ڵ�B���Գ�����x=��3�������������⣺
(1)�������ߵĽ���ʽ.
(2)����x��ƽ�е�ֱ���������߽���C��D���㣬��C�ڶԳ�����࣬��CD=8�����BCD�����.ע��������y=ax2+bx+c��a��0���ĶԳ�����x=��![]() .
.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com