
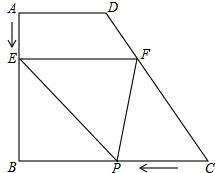
 如图,四边形ABCD中,AD∥BC,∠ABC=90°,AD=6,AB=8,BC=10,直线EF从AD出发,始终保持与AD平行,并以每秒1个单位的速度向BC移动,交AB于E,交CD于F,同时点P从C点出发,沿CB方向以每秒2个单位的速度向点B移动.当P点移动到点B时,停止运动,同时直线EF也停止运动,设移动时间为t秒,连接PF、PE,△PEF的面积为S.
如图,四边形ABCD中,AD∥BC,∠ABC=90°,AD=6,AB=8,BC=10,直线EF从AD出发,始终保持与AD平行,并以每秒1个单位的速度向BC移动,交AB于E,交CD于F,同时点P从C点出发,沿CB方向以每秒2个单位的速度向点B移动.当P点移动到点B时,停止运动,同时直线EF也停止运动,设移动时间为t秒,连接PF、PE,△PEF的面积为S.分析 (1)作DH⊥BC于H,交EF于G,如图,先根据矩形的性质得DG=AE=t,EG=BH=AD=6,DH=AB=8,则CH=BC-BH=4,再证明△DGF∽△DHC,利用相似比得到GF=$\frac{1}{2}$t,则EF=6+$\frac{1}{2}$t,根据平行四边形的判定,由于EF∥PC,则当EF=PC时,四边形EPCF为平行四边形,根据平行四边形的性质有PE∥CD,所以得到6+$\frac{1}{2}$t=2t,然后解方程求出t的值;
(2)由(1)得到EF=6+$\frac{1}{2}$t,BE=8-t,然后根据三角形面积公式求解;
(3)当△PEF的面积是梯形面积的$\frac{3}{4}$时,根据(2)的结论得到-$\frac{1}{4}$t2-t+24=$\frac{3}{4}$×$\frac{1}{2}$×(6+10)×8,然后含t一元二次方程的△<0,即可判定不存在某一时刻,使△PEF的面积是梯形ABCD面积的$\frac{3}{4}$.
解答 解:(1)作DH⊥BC于H,交EF于G,如图,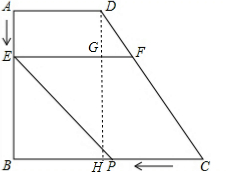 则DG=AE=t,EG=BH=AD=6,DH=AB=8,
则DG=AE=t,EG=BH=AD=6,DH=AB=8,
所以CH=BC-BH=4,
∵GF∥BC,
∴△DGF∽△DHC,
∴$\frac{GF}{HC}$=$\frac{DG}{DH}$,即$\frac{GF}{4}$=$\frac{t}{8}$,
∴GF=$\frac{1}{2}$t,
∴EF=EG+GF=6+$\frac{1}{2}$t,
∵EF∥PC,
∴当EF=PC时,四边形EPCF为平行四边形,则有PE∥CD,
即6+$\frac{1}{2}$t=2t,解得t=4,
即当t=4时,使PE∥CD;
(2)∵EF=6+$\frac{1}{2}$t,BE=8-t,
∴S=$\frac{1}{2}$•(6+$\frac{1}{2}$t)(8-t)
=-$\frac{1}{4}$t2-t+24(0≤t≤5);
(3)不存在.
当△PEF的面积是梯形面积的$\frac{3}{4}$时,则-$\frac{1}{4}$t2-t+24=$\frac{3}{4}$×$\frac{1}{2}$×(6+10)×8,
整理得t2+4t+96=0,
因为△=42-4×1×96<0
所以不存在某一时刻,使△PEF的面积是梯形ABCD面积的$\frac{3}{4}$.
点评 本题考查了四边形的综合题:熟练掌握梯形的性质、等腰直角三角形的判定和平行四边形的判定与性质;会利用相似比和三角形面积公式进行计算.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:填空题
 如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为$\frac{81π}{4}$.
如图,半圆O的直径AE=6,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD则图中阴影部分的面积为$\frac{81π}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com