
【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=![]() ,求PD的长.
,求PD的长.

【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)由圆周角定理可知∠ABC=∠BAC=60°,从而可证得△ABC是等边三角形;
(2)由△ABC是等边三角形可得出“AC=BC=AB=![]() ,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
试题解析:(1)∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC是等边三角形;
(2)∵△ABC是等边三角形,AB=![]() ,∴AC=BC=AB=
,∴AC=BC=AB=![]() ,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=
,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=![]() ,∴AP=ACcot∠APC=2.在Rt△DAC中,∠DAC=90°,AC=
,∴AP=ACcot∠APC=2.在Rt△DAC中,∠DAC=90°,AC=![]() ,∠ACD=60°,∴AD=ACtan∠ACD=6,∴PD=AD﹣AP=6﹣2=4.
,∠ACD=60°,∴AD=ACtan∠ACD=6,∴PD=AD﹣AP=6﹣2=4.


科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.

(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
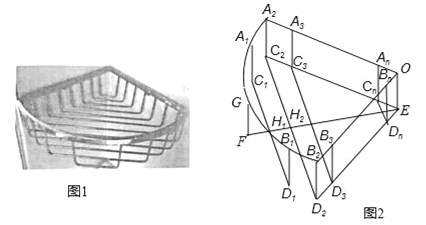
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.三角形两边之和大于第三边
查看答案和解析>>
科目:初中数学 来源: 题型:
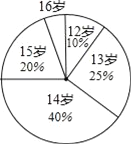
【题目】某中学抽样调查后得到n名学生年龄情况,将结果绘制成如图的扇形统计图.
(1)被调查学生年龄的中位数是_______,众数是________;
(2)被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数;
(3)通过计算求该学校学生年龄的平均数(精确到1岁).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为a,b,c,记![]() ,那么三角形的面积为
,那么三角形的面积为![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: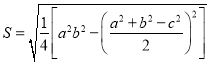 . ②
. ②
下面我们对公式②进行变形: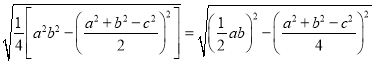
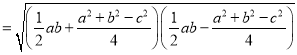
![]()
![]()
![]()
![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
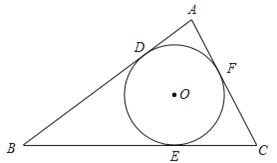
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市居民日平均用水量的调查
B.对一批LED节能灯使用寿命的调查
C.对重庆新闻频道“天天630”栏目收视率的调查
D.对某校九年级(1)班同学的身高情况的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明一个三角形中至少有两个锐角,首先我们可以假设( )
A.一个三角形中最多有三个锐角
B.一个三角形中最多有一个锐角
C.一个三角形中有一个角不是锐角
D.一个三角形中最多有两个锐角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com