
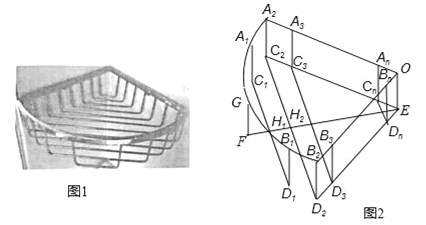
����Ŀ����ͼ1��һ������˿Χ�ɵ���������������һ�����Ƶ�������������ͼ2��������һ���뾶Ϊr��Բ�Ľ�90�������A2OB2������A2C2EO��B2D2EO�������ɸ�ȱһ�ߵľ���״��A1C1D1B1��A2C2D2B2������AnBnCnDn��OEFGΧ�ɣ�����A1��G��B1��![]() �ϣ�A2��A3����An��B2��B3����Bn�ֱ��ڰ뾶OA2��OB2�ϣ�C2��C3������Cn��D2��D3��Dn�ֱ���EC2��ED2�ϣ�EF��C2D2��H2��C1D1��EF��H1��FH1=H1H2=d��C1D1��C2D2��C3D3��CnDn���εȾ���ƽ���ŷţ����һ������״��ı�CnDn���E��ľ���Ӧ������d����A1C1��A2C2��A3C3�Ρ���AnCn��
�ϣ�A2��A3����An��B2��B3����Bn�ֱ��ڰ뾶OA2��OB2�ϣ�C2��C3������Cn��D2��D3��Dn�ֱ���EC2��ED2�ϣ�EF��C2D2��H2��C1D1��EF��H1��FH1=H1H2=d��C1D1��C2D2��C3D3��CnDn���εȾ���ƽ���ŷţ����һ������״��ı�CnDn���E��ľ���Ӧ������d����A1C1��A2C2��A3C3�Ρ���AnCn��
��1����d��ֵ��
��2���ʣ�CnDn���E��ľ����ܷ����d������ܣ����������n��ֵ��������ܣ���ô����֮��ľ����Ƕ��٣�
���𰸡���1��![]() ����2�����ܣ�
����2�����ܣ�![]() ��
��
��������
�����������1������d=![]() FH2�����EH2���ɽ�����⣮
FH2�����EH2���ɽ�����⣮
��2������CnDn���E��ľ����ܵ���d���г�����n�ķ�����⣬����nû�������⣬��![]() =
=![]() ��4.8�����n���ɽ�����⣮
��4.8�����n���ɽ�����⣮
�����������1����RT��D2EC2�У��ߡ�D2EC2=90�㣬EC2=ED2=r��EF��C2D2����EH1=![]() r��FH1=r��
r��FH1=r��![]() r����d=
r����d=![]() =
=![]() ��
��
��2������CnDn���E��ľ����ܵ���d��������![]() ���������nû�������⣬���Լ��費������
���������nû�������⣬���Լ��費������
��![]() =
=![]() ��4.8����n=6����ʱCnDn���E��ľ���=
��4.8����n=6����ʱCnDn���E��ľ���=![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽ��,�ϳ���һ����23 cm,�϶̵�һ����15 cm.������ֽ������ͬ������һ�κ�,ʣ�µ�����ֽ����,Ҫ��ϳ���ֽ���ij��Ȳ����ڽ϶̵�ֽ�����ȵ�����,��ô���µij���������( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и������У��ܹ���ֱ�������ε����ߵij��ǣ� ��
A.3��5��5
B.3��4��5
C.5��12��15
D.5��24��25
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���ⷽ��x2+2x��5=0ʱ��ԭ����Ӧ����Ϊ�� ��
A.��x+1��2=6
B.��x��1��2=6
C.��x+2��2=9
D.��x��2��2=9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������P����AC��һ���㣨����A��C�غϣ�������P��PE��AB������ΪE������EP��![]() �ڵ�F��������C�������ڵ�D��
�ڵ�F��������C�������ڵ�D��
��1����֤��DC=DP��
��2������CAB=30�㣬��F��![]() ���е�ʱ���ж���A��O��C��FΪ������ı�����ʲô�����ı��Σ�˵��������
���е�ʱ���ж���A��O��C��FΪ������ı�����ʲô�����ı��Σ�˵��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ȱ������α߳�����ֵ�Ƿ���x2��3x��10��0�ĸ�����ô��������ε��ܳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��P��B��C��Բ�ϵ��ĸ��㣬��APC=��CPB=60�㣬AP��CB���ӳ����ཻ�ڵ�D��
��1����֤����ABC�ǵȱ������Σ�
��2������PAC=90�㣬AB=![]() ����PD�ij���
����PD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2+2x+3�Ķ�����Ϊ�� ��
A.x��0
B.xΪһ��ʵ��
C.y��2
D.yΪһ��ʵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������11�·ݼס��ҡ����������е�ƽ�����·ֱ�Ϊ��5�桢��1�桢15�棬��ô��ߵ�ƽ�����±���͵�ƽ�����¸ߣ� ��
A. 10�� B. 14�� C. 16�� D. 20��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com