
【题目】某学校为了解学生课外阅读的情况,对学生“平均每天课外阅读的时间”进行了随机抽样调查,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题: 
(1)平均每天课外阅读的时间为“0.5~1小时”部分的扇形图的圆心角为多少度;
(2)本次一共调查了多少名学生;
(3)将条形图补充完整;
(4)若该校有1680名学生,请估计该校有多少名学生平均每天课外阅读的时间在0.5小时以下.
【答案】
(1)解:每天课外阅读的时间为“0.5~1小时”的学生所占的比例是:1﹣50%﹣30%﹣5%=15%,
则时间为“0.5~1小时”部分的扇形图的圆心角为:15%×360°=54°,
故答案是:54;
(2)解:调查的总人数是:100÷50%=200,
故答案是:200;
(3)解:

(4)解:在0.5小时以下的人数:1680×5%=84(人).
【解析】(1)首先求出每天课外阅读的时间为“0.5~1小时”的学生所占的比例,然后乘以360°,即可求解;(2)平均每天课外阅读的时间在1~1.5小时的有100人,占50%,据此即可求得总人数;(3)利用1680人乘以所占的比例即可求解.
【考点精析】根据题目的已知条件,利用扇形统计图和条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.


科目:初中数学 来源: 题型:
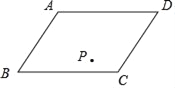
【题目】现有一块平行四边形田地ABCD要平均分给甲、乙两人,由于在这块地里有一口水井P,如图所示,为了甲,乙两人都能方便使用这口井,请你用所学的数学知识帮助甲,乙两人平均划分该田地.
要求:作图,写出划分方案,并证明你的划分方案符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
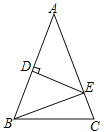
【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,AC为⊙O的直径,PO交于⊙O于点E. 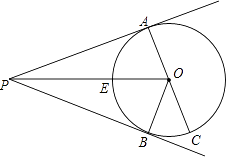
(1)试判断∠APB与∠BAC的数量关系;
(2)若⊙O的半径为4,P是⊙O外一动点,是否存在点P,使四边形PAOB为正方形?若存在,请求出PO的长,并判断点P的个数及其满足的条件;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数 ![]() 的图象交EF于点B,则点B的坐标为 .
的图象交EF于点B,则点B的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机上网已经成为当今年轻人时尚的网络生活,某网络公司看中了这种商机,推出了两种手机上网的计费方式:方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设某客户月手机上网的时间为x分钟,上网费用为y元. 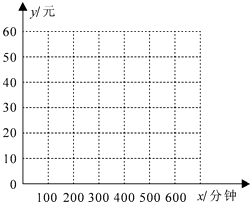
(1)分别写出该客户按A、B两种方式的上网费y(元)与每月上网时间x(分钟)的函数关系式,并在右图的坐标系中画出这两个函数的图象;
(2)如何选择计费方式能使该客户上网费用更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=﹣ ![]() x2+
x2+ ![]() x+4经过A、B两点.
x+4经过A、B两点.
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是
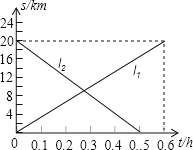
A. 乙摩托车的速度较快
B. 经过0.3小时甲摩托车行驶到A,B两地的中点
C. 经过0.25小时两摩托车相遇
D. 当乙摩托车到达A地时,甲摩托车距离A地![]() km
km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)已知A,B两地相距200千米,一辆汽车以每小时60千米的速度从A地匀速驶往B地,到达B地后不再行驶,设汽车行驶的时间为x小时,汽车与B地的距离为y千米.
(1)求y与x的函数关系,并写出自变量x的取值范围;
(2)当汽车行驶了2小时时,求汽车距B地有多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com