
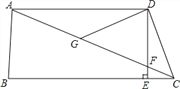
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
(1)说明DC=DG;
(2)若DG=7,EC=4,求DE的长.
【答案】(1)说明见解析;(2)![]() .
.
【解析】试题分析:(1)根据直角三角形斜边上的中线的性质可得DG=AG,根据等腰三角形的性质可得∠GAD=∠GDA,根据三角形外角的性质可得∠CGD=2∠GAD,再根据平行线的性质和等量关系可得∠ACD=∠CGD,根据等腰三角形的性质可得CD=DG;
(2)根据勾股定理即可求解.
试题解析:(1)证明:∵DE⊥BC,
∴∠DEB=90°,
∵AD∥BC,
∴∠ADE+∠DEB=180°,
∴∠ADE=90°,
∵G为AF的中点,
∴DG=AG,
∴∠DAF=∠ADG,
∴∠DGC=∠DAF+∠ADG=2∠DAC,
∵AD∥BC,
∴∠ACB=∠DAC,
∵∠ACD=2∠ACB,
∴∠DGC=∠DCA,
∴DC=DG;
(2)解:∵在Rt△DEC中,∠DEC=90°,DG=DC=5,CE=2,
∴由勾股定理得:DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示:
(1)填空:甲种收费的函数关系式是 ;乙种收费的函数关系式是 ;
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OE平分∠AOC,OF平分∠BOC 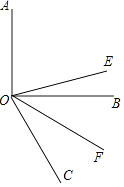
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数.
(2)若∠AOC=x°,∠EOF=y°,∠BOC=60°,请用x 的代数式来表示y.(直接写出结果就行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=120°,射线OA绕点O以每秒钟6°的速度逆时针旋转到OP,设射线OA旋转OP所用时间为t秒(t<30). 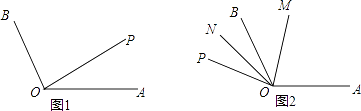
(1)如图1,直接写出∠BOP=°(用含t的式子表示);
(2)若OM平分∠AOP,ON平分∠BOP. ①当OA旋转到如图1所示OP处,请完成作图并求∠MON的度数;
②当OA旋转到如图2所示OP处,若2∠BOM=3∠BON,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
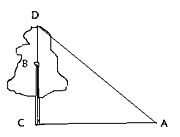
【题目】如图,在一棵树上10m高的B处有两只猴子,其中一只猴子沿树爬下,走到离树20m 处的池塘A处,另一只猴子爬到树顶D处直跃向池塘的A处,如果两只猴子所经过的路程相等,则这颗树有多高(设树与地面垂直)?
查看答案和解析>>
科目:初中数学 来源: 题型:
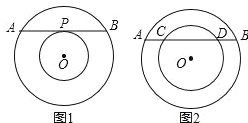
【题目】圆心相同,半径不相等的两个圆叫做同心圆,用大圆的面积减去小圆的面积就是圆环的面积.
(1)如图1,大圆的弦AB切小圆于点P,求证:AP=BP;
(2)若AB=2a,请用含有a的代数式表示图1中的圆环面积;
(3)如图2,若大圆的弦AB交小圆于C、D两点,且AB=8,CD=6,则圆环的面积为 ____ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0
(1)求证:方程有两个实数根;
(2)当k为何值时,此方程的两个实数根互为相反数;
(3)我们定义:若一元二次方程ax2+bx+c=0的两个正实数根x1、x2(x1>x2),满足2<![]() <3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
<3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com