
【题目】已知:关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0
(1)求证:方程有两个实数根;
(2)当k为何值时,此方程的两个实数根互为相反数;
(3)我们定义:若一元二次方程ax2+bx+c=0的两个正实数根x1、x2(x1>x2),满足2<![]() <3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
<3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
【答案】(1)证明见解析(2)1(3)﹣![]() <k<-
<k<-![]() 或﹣3<k<﹣2
或﹣3<k<﹣2
【解析】
试题分析:(1)根据方程的判别式,可得答案;
(2)根据互为相反数的和为零,可得关于k的方程,根据解方程,可得答案;
(3)根据方程的梦想根,可得不等式组,根据解不等式组,可得答案.
试题解析:(1)关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0,
a=k,b=﹣(k﹣1),c=﹣1,
△=b2﹣4ac=[﹣(k﹣1)]2﹣4k(﹣1)=k2+2k+1=(k+1)2≥0,
关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个实数根;
(2)关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0,
x1=![]() ,x2=
,x2=![]() ,
,
方程的两个实数根互为相反数,得
x1+x2=![]() +
+![]() =0,
=0,
即![]() =0,
=0,
解得k=1,
当k=1时,此方程的两个实数根互为相反数;
(3)当k>0时,x1=1,x2=﹣![]() <0,不符合题意;
<0,不符合题意;
当﹣1≤k<0时,x1=﹣![]() ,x2=1,2<
,x2=1,2<![]() <3,得
<3,得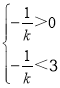 ,
,
解得﹣![]() <k<-
<k<-![]() ;
;
当k<﹣1时,x1=﹣![]() ,x2=1,由2<
,x2=1,由2<![]() <3,得2<﹣k<3,
<3,得2<﹣k<3,
解得﹣3<k<﹣2不符合题意舍去,
综上所述:于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,k的范围是:
﹣![]() <k<-
<k<-![]() 或﹣3<k<﹣2.
或﹣3<k<﹣2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
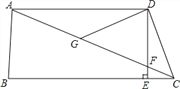
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
(1)说明DC=DG;
(2)若DG=7,EC=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月24日上午9时港珠澳大桥正式通车,它是东亚建设的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,整个大桥造价超过720亿元人民币,将72000000000用科学记数法表示为( )
A.7.2×1011B.7.2×1010C.0.72×1011D.72×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①有理数包括整数和分数;
②一个代数式不是单项式就是多项式;
③几个有理数相乘,若负因数的个数是偶数个,则积为正数;
④倒数等于本身的数有﹣1.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com