练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

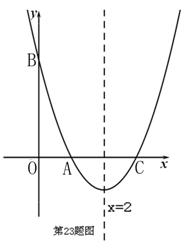
    如图,抛物线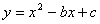交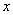轴于点A(1,0),交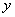轴于点B,对称轴是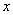=2.

    （1）求抛物线的解析式.

    （2）点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小？若存在,求出点P的坐标；若不存在,请说明理由.                          

     



    解：（1）根据题意得 C(3，0)……………………………………………………1分

    9-3b+c=0

    1-b+c=0    …………………………………………………………1分

         

    解得

    b=4    

    c=3           ………………………………………………………1分   

    所以二次函数的解析式为y=x2－4x+3  …………………………………1分

     (2) 设BC解析式为y=kx+b (k≠0)

         根据题意:    解得:      ∴………1分

         当x=2时,y=1

         ∴ P（2，1）                    …………………………………1分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    2015年某中学举行的春季田径径运动会上，参加男子跳高的15名运动员的成绩如表所示：

    成绩（m）

    1.80

    1.50

    1.60

    1.65

    1.70

    1.75

    人数

    1

    2

    4

    3

    3

    2

    这些运动员跳高成绩的中位数和众数分别是（　　）

    　

    A．

    1.70m，1.65m

    B．

    1.70m，1.70m

    C．

    1.65m，1.60m

    D．

    3，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


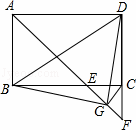
    如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：

    ①BE=CD；

    ②∠DGF=135°；

    ③∠ABG+∠ADG=180°；

    ④若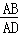=，则3S△BDG=13S△DGF．

    其中正确的结论是　 　．（填写所有正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列各运算中，计算正确的是                                       （     ）                                               

    A.   B.  C.(-2)-1=2  D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是  (      )

    A.4.8       B.4.8或3.8      C.3.8       D.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图,四边形OABC是矩形,点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在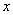轴上，直线BD交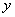轴于点F,交OE于点H,线段BC、OC的长是方程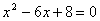的两个根，且OC＞BC.

    （1）求直线BD的解析式.

    （2）求 △OFH的面积.

    （3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个不透明的盒子里装有3个黑球和1个白球，每个球除颜色外都相同，从中任意摸出2个球，下列事件中，不可能事件是（　　）

    　  A．摸出的2个球都是白球             B． 摸出的2个球有一个是白球

    　  C．摸出的2个球都是黑球             D． 摸出的2个球有一个黑球

    查看答案和解析>>

    科目：初中数学 来源： 题型：


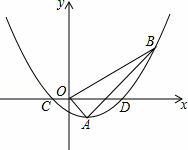
    如图，在平面直角坐标系中，顶点为A（1，﹣1）的抛物线经过点B（5，3），且与x轴交于C，D两点（点C在点D的左侧）．

    （1）求抛物线的解析式；

    （2）求点O到直线AB的距离；

    （3）点M在第二象限内的抛物线上，点N在x轴上，且∠MND=∠OAB，当△DMN与△OAB相似时，请你直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB=　 　．

    查看答案和解析>>

    同步练习册答案