
如图,四 边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在
边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在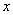 轴上,直线BD交
轴上,直线BD交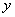 轴于点F,交OE于点H,线段BC、OC的长是方程
轴于点F,交OE于点H,线段BC、OC的长是方程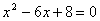 的两个根,且OC>BC.
的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求 △OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
 |
解:(1)x2-6x+8=0
x1=2,x2=4
∵OC > BC
∴OC=4,BC=2
B(-2,4)
∵OD=OC=4 ∴D(4,0) …………………………………………………………1分
设BD解析式为y=kx+b (k≠0)
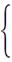
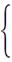 ∴ -2k+b=4 ∴ k=
∴ -2k+b=4 ∴ k=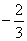 ………………………………2分
………………………………2分
4k+b=0 b=
b=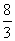
∴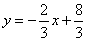 ………………………………………………1分
………………………………………………1分
(2) ∵DE=2, ∴E(4,2)∴直线OE:y=
 …………………………………………1分
…………………………………………1分
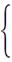 ∴
∴ 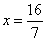
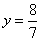
∴H(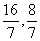 ) ………………………………………1分
) ………………………………………1分
当x=0,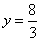 ∴S△OFH =
∴S△OFH =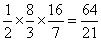 ………………………………………1分
………………………………………1分
(3) 存在N1(4,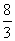 ),N2(
),N2(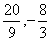 ), N3(-4,-
), N3(-4,-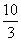 ) …………………………………3分
) …………………………………3分


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是( )
|
| A. | a(x0﹣x1)(x0﹣x2)<0 | B. | a>0 |
|
| C. | b2﹣4ac≥0 | D. | x1<x0<x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
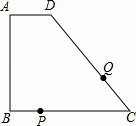
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
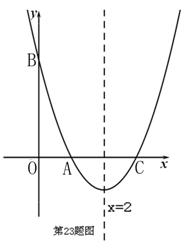
如图,抛物线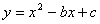 交
交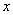 轴于点A(1,0),交
轴于点A(1,0),交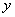 轴于点B,对称轴是
轴于点B,对称轴是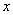 =2.
=2.
(1)求抛物线的解析式.
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在九(1)班的一次体育测试中,某小组7位女生的一分钟跳绳次数分别是:162,167,158,165,175,142,167,这组数据的中位数是( )
A.156 B. 162 C. 165 D. 167
查看答案和解析>>
科目:初中数学 来源: 题型:
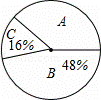
某班数学老师想了解学生对数学的喜欢程度,对全班50名学生进行调查,根据调查结果绘制了扇形统计图(如图所示),其中A表示“很喜欢”,B表示“一般”,C表示“不喜欢”,则该班“很喜欢”数学的学生有 人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com