
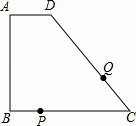
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长.
解:(1)如图1,作DE⊥BC于E,
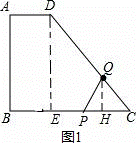
∵AD∥BC,∠A=90°,
∴四边形ABED为矩形,
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴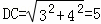 厘米;
厘米;
(2)∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴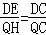 ,
,
∴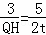 ,
,
∴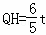 ,
,
∴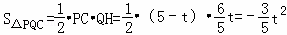 ,
,
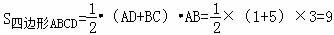 ,
,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,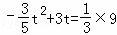 ,
,
即t2﹣5t+5=0,
解得: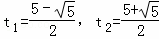 (舍去);
(舍去);
②S△PQC:S四边形ABCD=2:3时,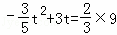 ,
,
即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为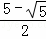 秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
(3)如图2,
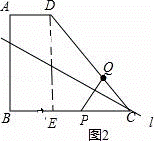
①当PQ的垂直平分线l经过点C时,可知PC=QC,
∴5﹣t=2t,
∴3t=5,
∴t=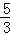 ,
,
∴当t= 秒时,直线l经过点C;
秒时,直线l经过点C;
②如图3,
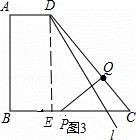
当PQ的垂直平分线l经过点D时,
可知DQ=DP,
连接DP,则在Rt△DEP中,DP2=DE2+EP2,
∴DQ2=DE2+EP2,
∴(5﹣2t)2=32+(t﹣1)2,
∴t1=1,t2=5(舍去),
∴BP=1厘米,
∴当t=1秒时,直线l经过点D,此时点P与点E重合;
如图4,连接FQ,
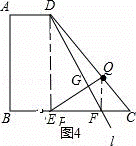
∵直线l是△DPQ的对称轴,
∴△DEF≌△DQF,∠DQF=90°,EF=QF,
设EF=x厘米,则QF=x厘米,FC=(4﹣x)厘米,
在Rt△FQC中,FQ2+QC2=FC2,
x2+22=(4﹣x)2,
∴x=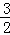 ,
,
∴EF=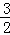 厘米,
厘米,
在Rt△DEF中,DE2+EF2=DF2,
∴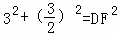 ,
,
∴DF= 厘米,
厘米,
在Rt△DEF中,EG⊥DF,
∴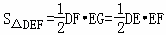 ,
,
∴EG=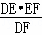 ,
,
∴EG=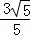 厘米,
厘米,
∴PQ=2EG=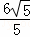 厘米.
厘米.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.( 取1.732,结果保留整数)
取1.732,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
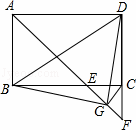
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若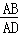 =
= ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.
其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,四 边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在
边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在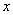 轴上,直线BD交
轴上,直线BD交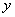 轴于点F,交OE于点H,线段BC、OC的长是方程
轴于点F,交OE于点H,线段BC、OC的长是方程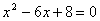 的两个根,且OC>BC.
的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求 △OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com