
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.( 取1.732,结果保留整数)
取1.732,结果保留整数)

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
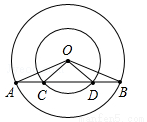
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.
(1)求证:CF=CH;
(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
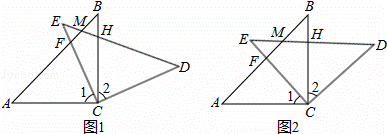
查看答案和解析>>
科目:初中数学 来源: 题型:
若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是( )
|
| A. | a(x0﹣x1)(x0﹣x2)<0 | B. | a>0 |
|
| C. | b2﹣4ac≥0 | D. | x1<x0<x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在直角坐标系中,直线y=x+1与y轴交于点 A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
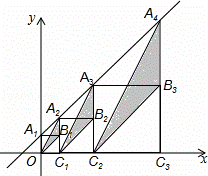
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中正确的是( )
A. 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为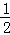
B. “对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件
C. “同位角相等”这一事件是不可能事件
D. “钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
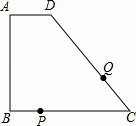
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
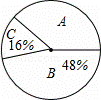
某班数学老师想了解学生对数学的喜欢程度,对全班50名学生进行调查,根据调查结果绘制了扇形统计图(如图所示),其中A表示“很喜欢”,B表示“一般”,C表示“不喜欢”,则该班“很喜欢”数学的学生有 人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com