
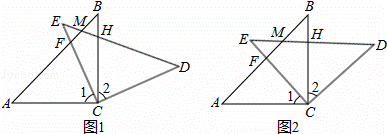
如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.
(1)求证:CF=CH;
(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
(1)证明:∵AC=CE=CB=CD,∠ACB=∠ECD=90°,
∴∠A=∠B=∠D=∠E=45°.
在△BCF和△ECH中,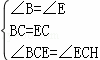 ,
,
∴△BCF≌△ECH(ASA),
∴CF=CH(全等三角形的对应边相等);
(2)解:四边形ACDM是菱形.
证明:∵∠ACB=∠DCE=90°,∠BCE=45°,
∴∠1=∠2=45°.
∵∠E=45°,
∴∠1=∠E,
∴AC∥DE,
∴∠AMH=180°﹣∠A=135°=∠ACD,
又∵∠A=∠D=45°,
∴四边形ACDM是平行四边形(两组对角相等的四边形是平行四边形),
∵AC=CD,
∴四边形ACDM是菱形.
点评: 菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:
①定义;
②四边相等;
③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.


科目:初中数学 来源:2014-2015学年江苏省无锡市天一实验学校九年级中考一模数学试卷(解析版) 题型:解答题
(本题满分8分)小英与她的父亲、母亲计划清明小长假外出旅游,初步选择了苏州、常州、上海、南京四个城市,由于时间仓促,他们只能去其中一个城市,到底去哪一个城市三个人意见不统一,在这种情况下,小英父亲建议,用小英学过的摸球游戏来决定,规则如下:
①在一个不透明的袋子中装一个红球(苏州)、一个白球(常州)、一个黄球(上海)和一个黑球(南京),这四个球除颜色不同外,其余完全相同;
②小英父亲先将袋中球摇匀,让小英从袋中随机摸出一球,父亲记录下其颜色,并将这个球放回袋中摇匀,然后让小英母亲从袋中随机摸出一球,父亲记录下它的颜色;
③若两人所摸出球的颜色相同,则去该球所表示的城市旅游,否则,前面的记录作废,按规则②重新摸球,直到两人所摸出球的颜色相同为止.
按照上面的规则,请你解答下列问题:
(1)已知小英的理想旅游城市是常州,小英和母亲随机各摸球一次,,请用画树状图或列表法求两人均摸出白球的概率是多少?
(2)已知小英母亲的理想旅游城市是上海,小英和母亲随机各摸球一次,至少有一人摸出黄球的概率是多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB 上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )

A.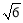 B.
B.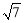 C.2
C.2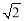 D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年某中学举行的春季田径径运动会上,参加男子跳高的15名运动员的成绩如表所示:
| 成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
|
| A. | 1.70m,1.65m | B. | 1.70m,1.70m | C. | 1.65m,1.60m | D. | 3,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.( 取1.732,结果保留整数)
取1.732,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com