
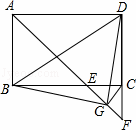
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若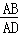 =
= ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.
其中正确的结论是 .(填写所有正确结论的序号)
①③④. 解:∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,
故①正确;
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
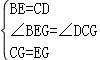 ,
,
∴△DCG≌△BEG(SAS).
∴∠BGE=∠DGC,
∵∠BGE<∠AEB,
∴∠DGC=∠BGE<45°,
∵∠CGF=90°,
∴∠DGF<135°,
故②错误;
∵∠BGE=∠DGC,
∴∠ABG+∠ADG=∠ABC+∠CBG+∠ADC﹣∠CDG=∠ABC+∠ADC=180°,
故③正确;
∵△DCG≌△BEG,
∵∠BGE=∠DGC,BG=DG,
∵∠EGC=90°,
∴∠BGD=90°,
∵BD=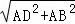 =
=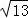 ,
,
∴BG=DG=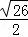 ,
,
∴S△BDG=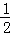 ×
×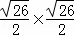 =
=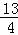
∴3S△BDG=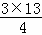 ,
,
过G作GM⊥CF于M,
∵CE=CF=BC﹣BE=BC﹣AB=1,
∴GM=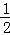 CF=
CF=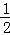 ,
,
∴S△DGF=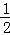 •DF•GM=
•DF•GM=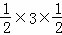 =
=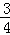 ,
,
∴13S△DGF=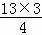 ,
,
∴3S△BDG=13S△DGF,
故④正确.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
在“百度”搜索引擎中输入“姚明”,能搜索到与之相关的网页约27000000个,将这个数用科学记 数法表示为( )
数法表示为( )
A. 2.7×105 B. 2.7×106 C. 2.7×107 D. 2.7×108
查看答案和解析>>
科目:初中数学 来源: 题型:
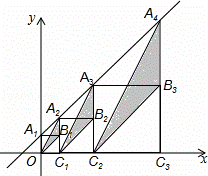
在直角坐标系中,直线y=x+1与y轴交于点 A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中正确的是( )
A. 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为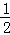
B. “对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件
C. “同位角相等”这一事件是不可能事件
D. “钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
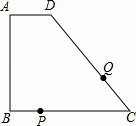
如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
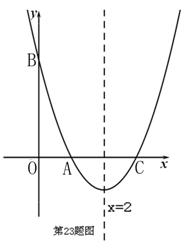
如图,抛物线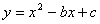 交
交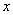 轴于点A(1,0),交
轴于点A(1,0),交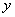 轴于点B,对称轴是
轴于点B,对称轴是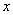 =2.
=2.
(1)求抛物线的解析式.
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com