练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

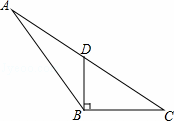
    如图，在△ABC中，D为AC边的中点，且DB⊥BC，BC=4，CD=5．

    （1）求DB的长；

    （2）在△ABC中，求BC边上高的长．


        解：（1）∵DB⊥BC，BC=4，CD=5，

    ∴BD==3；

    （2）延长CB，过点A作AE⊥CB延长线于点E，

    ∵DB⊥BC，AE⊥BC，

    ∴AE∥DB，

    ∵D为AC边的中点，

    ∴BD=AE，

    ∴AE=6，即BC边上高的长为6．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图,四边形OABC是矩形,点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在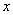轴上，直线BD交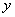轴于点F,交OE于点H,线段BC、OC的长是方程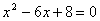的两个根，且OC＞BC.

    （1）求直线BD的解析式.

    （2）求 △OFH的面积.

    （3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


        如题16图，△ABC三边的中线AD，BE，CF的公共点G，若，则图中阴影部分面积是          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在下列单项式中，与2xy是同类项的是（　　）

    　  A． 2x2y2          B． 3y                C． xy                D． 4x

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知抛物线y=﹣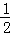（x2﹣7x+6）的顶点坐标为M，与x轴相交于A，B两点（点B在点A的右侧），与y轴相交于点C．

    （1）用配方法将抛物线的解析式化为顶点式：y=a（x﹣h）2+k（a≠0），并指出顶点M的坐标；

    （2）在抛物线的对称轴上找点R，使得CR+AR的值最小，并求出其最小值和点R的坐标；

    （3）以AB为直径作⊙N交抛物线于点P（点P在对称轴的左侧），求证：直线MP是⊙N的切线．

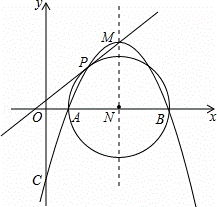
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某校在体育健康测试中，有8名男生“引体向上”的成绩（单位：次）分别是：14，12，8，9，16，12，7，这组数据的中位数和众数分别是（　　）

    　 A． 10，12 B． 12，11 C． 11，12 D． 12，12

    查看答案和解析>>

    科目：初中数学 来源： 题型：


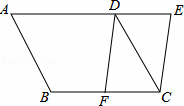
    如图，将▱ABCD的AD边延长至点E，使DE=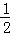AD，连接CE，F是BC边的中点，连接FD．

    （1）求证：四边形CEDF是平行四边形；

    （2）若AB=3，AD=4，∠A=60°，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，则的值为         2

    ．

    查看答案和解析>>

    同步练习册答案