
如图,已知抛物线y=﹣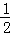 (x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(x2﹣7x+6)的顶点坐标为M,与x轴相交于A,B两点(点B在点A的右侧),与y轴相交于点C.
(1)用配方法将抛物线的解析式化为顶点式:y=a(x﹣h)2+k(a≠0),并指出顶点M的坐标;
(2)在抛物线的对称轴上找点R,使得CR+AR的值最小,并求出其最小值和点R的坐标;
(3)以AB为直径作⊙N交抛物线于点P(点P在对称轴的左侧),求证:直线MP是⊙N的切线.
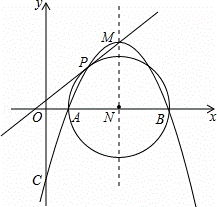
(1)解:∵y=﹣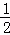 (x2﹣7x+6)=﹣
(x2﹣7x+6)=﹣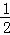 (x2﹣7x)﹣3=﹣
(x2﹣7x)﹣3=﹣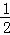 (x﹣
(x﹣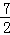 )2+
)2+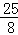 ,
,
∴抛物线的解析式化为顶点式为:y=﹣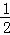 (x﹣
(x﹣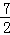 )2+
)2+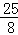 ,
,
顶点M的坐标是(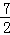 ,
,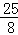 );
);
(2)解:∵y=﹣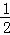 (x2﹣7x+6),
(x2﹣7x+6),
∴当y=0时,﹣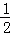 (x2﹣7x+6)=0,
(x2﹣7x+6)=0,
解得x=1或6,
∴A(1,0),B(6,0),
∵x=0时,y=﹣3,
∴C(0,﹣3).
连接BC,则BC与对称轴x= 的交点为R,连接AR,
的交点为R,连接AR,
则CR+AR=CR+BR=BC,根据两点之间线段最短可知此时CR+AR的值最小,
最小值为BC=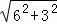 =3
=3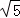 .
.
设直线BC的解析式为y=kx+b,
∵B(6,0),C(0,﹣3),
∴ ,
,
解得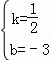 ,
,
∴直线BC的解析式为:y=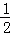 x﹣3,
x﹣3,
令x= ,得y=
,得y=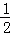 ×
×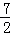 ﹣3=﹣
﹣3=﹣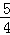 ,
,
∴R点坐标为(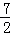 ,﹣
,﹣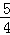 );
);
(3)证明:设点P坐标为(x,﹣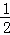 x2+
x2+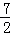 x﹣3).
x﹣3).
∵A(1,0),B(6,0),
∴N(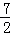 ,0),
,0),
∴以AB为直径的⊙N的半径为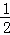 AB=
AB=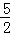 ,
,
∴NP=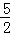 ,
,
即(x﹣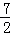 )2+(﹣
)2+(﹣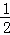 x2+
x2+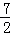 x﹣3)2=(
x﹣3)2=(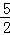 )2,
)2,
化简整理得,x4﹣14x3+65x2﹣112x+60=0,
(x﹣1)(x﹣2)(x﹣5)(x﹣6)=0,
解得x1=1(与A重合,舍去),x2=2,x3=5(在对称轴的右侧,舍去),x4=6(与B重合,舍去),
∴点P坐标为(2,2).
∵M(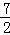 ,
,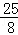 ),N(
),N(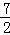 ,0),
,0),
∴PM2=(2﹣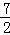 )2+(2﹣
)2+(2﹣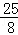 )2=
)2=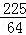 ,
,
PN2=(2﹣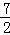 )2+22=
)2+22=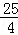 =
=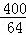 ,
,
MN2=(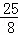 )2=
)2= ,
,
∴PM2+PN2=MN2,
∴∠MPN=90°,
∵点P在⊙N上,
∴直线MP是⊙N的切线.



科目:初中数学 来源: 题型:
在九(1)班的一次体育测试中,某小组7位女生的一分钟跳绳次数分别是:162,167,158,165,175,142,167,这组数据的中位数是( )
A.156 B. 162 C. 165 D. 167
查看答案和解析>>
科目:初中数学 来源: 题型:
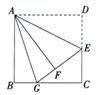
如题21图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延 长交BC于点G,连接AG.
(1) 求证:△ABG≌△AFG;
(2) 求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年我市有1.6万名初中毕业生参加升学考试,为了了解这1.6万名考生的数学成绩,从中抽取2000名考生的数学成绩进行统计,在这个问题中样本是( )
A.1.6万名考生 B. 2000名考生
C.1.6万名考生的数学成绩 D. 2000名考生的数学成 绩
绩
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com