练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将▱ABCD的AD边延长至点E，使DE=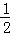AD，连接CE，F是BC边的中点，连接FD．

    （1）求证：四边形CEDF是平行四边形；

    （2）若AB=3，AD=4，∠A=60°，求CE的长．


     （1）证明：∵四边形ABCD是平行四边形，

    ∴AD=BC，AD∥BC，

    ∵DE=AD，F是BC边的中点，

    ∴DE=FC，DE∥FC，

    ∴四边形CEDF是平行四边形；

    （2）解：过点D作DN⊥BC于点N，

    ∵四边形ABCD是平行四边形，∠A=60°，

    ∴∠BCD=∠A=60°，

    ∵AB=3，AD=4，

    ∴FC=2，NC=DC=，DN=，

    ∴FN=，则DF=EC==．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


        如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是

    A.75°              B.55°              C.40°              D.35°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，D为AC边的中点，且DB⊥BC，BC=4，CD=5．

    （1）求DB的长；

    （2）在△ABC中，求BC边上高的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若关于x的一元二次方程x2+（2k﹣1）x+k2﹣1=0有实数根，则k的取值范围是（　　）

    　 A． k≥ B． k＞ C． k＜ D． k≤

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，交BC于点D，若CD=1，则BD=　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     2015年我市有1.6万名初中毕业生参加升学考试，为了了解这1.6万名考生的数学成绩，从中抽取2000名考生的数学成绩进行统计，在这个问题中样本是（　　）

    　  A．1.6万名考生                      B． 2000名考生

    　  C．1.6万名考生的数学成绩            D． 2000名考生的数学成绩

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的一元二次方程（m﹣2）x2+（2m+1）x+m﹣2﹣0有两个不相等的正实数根，则m的取值范围是（　　）

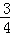    　  A．m＞         B． m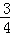＞且m≠2     C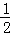． ﹣＜m＜2       D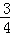． ＜m＜2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，直线l1和直线l2被直线l所截，已知

    l1∥l2，∠1＝70°，则∠2＝（　　）

    A．110°     B．90°     C．70°     D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：；

    查看答案和解析>>

    同步练习册答案