
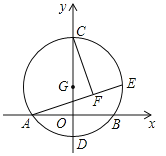
【题目】如图,以![]() 为圆心,半径为
为圆心,半径为![]() 的圆与
的圆与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 为⊙
为⊙![]() 上一动点,
上一动点,![]() 于
于![]() ,则弦
,则弦![]() 的长度为__________,当点
的长度为__________,当点![]() 在⊙
在⊙![]() 上运动的过程中,线段
上运动的过程中,线段![]() 的长度的最小值为__________.
的长度的最小值为__________.
【答案】 ![]() ;
; ![]()
【解析】作GM⊥AC于M,连接AG.因为∠AFC=90°,推出点F在以AC为直径的⊙M上,推出当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM,想办法求出FM、GM即可解决问题;
作GM⊥AC于M,连接AG.
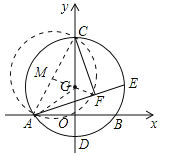
∵GO⊥AB,∴OA=OB.在Rt△AGO中,∵AG=2,OG=1,∴AG=2OG,OA=![]() =
=![]() ,∴∠GAO=30°,AB=2AO=2
,∴∠GAO=30°,AB=2AO=2![]() ,∴∠AGO=60°.
,∴∠AGO=60°.
∵GC=GA,∴∠GCA=∠GAC.
∵∠AGO=∠GCA+∠GAC,∴∠GCA=∠GAC=30°,∴AC=2OA=2![]() ,MG=
,MG=![]() CG=1.
CG=1.
∵∠AFC=90°,∴点F在以AC为直径的⊙M上,当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=![]() ﹣1.
﹣1.
故答案为:2![]() ﹣1.
﹣1.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
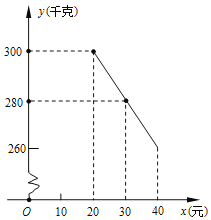
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x 的函数关系图象.
(1)求y与x的函数关系式;
(2)直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)![]() ,其中
,其中![]()
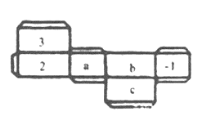
(2)如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
①填空:![]() _________,
_________,![]() _________
_________![]() _________;
_________;
②先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD,求作菱形AECF,使点E、点F分别在BC、AD边上
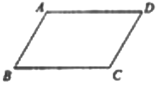
下面是小明设计的尺规作图过程.
作法:如图
① 连接AC;
② 分别以A、C为圆心,大于![]() AC的长为半径作弧,两弧交于M、N两点;
AC的长为半径作弧,两弧交于M、N两点;
③ 连接MN,分别与BC、AD、AC交于E、F、O三点;
④ 连接AE、CF
四边形AECF即为所求
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明
证明∵AM= ,AN= ,
∴MN是AC的垂直平分线。
( )(填推理的依据)
∴EF⊥AC,OA=OC,
∴平行四边形ABCD
∴AD∥BC
∴∠FAO=∠ECO
在△FAO和△ECO中

∴△FAO≌△ECO
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
( )(填推理依据)
∵EF⊥AC
∴四边形AECF是菱形
( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.
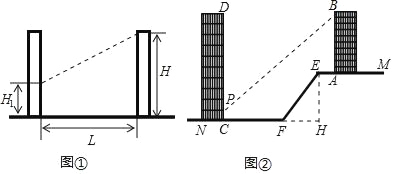
如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.
(1)求山坡EF的水平宽度FH;
(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市管理部门对“十一”国庆放假期间七天本市某景区客流变化量进行了不完全统计,数据如下(用正数表示客流量比前一天增加,用负数表示客流量比前一天下降):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
变化(万人) |
|
|
|
|
|
|
|
请通过计算解决以下问题:
(1)请判断这7天中,哪一天人数最多?哪一天人数最少?
(2)与10月3日相比,10月5日的客流量是上升了还是下降了?
(3)如图9月30日的客流量为1.5万人,据统计平均每人每天消费200元,请问该景区在“十一”七天国庆假期的总收入为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线,便把正方形分成
条横线,便把正方形分成![]() 部分(如图①);如果在正方形中画
部分(如图①);如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线,便把正方形分成
条横线,便把正方形分成![]() 部分(如图②);如果在正方形中画
部分(如图②);如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线,便把正方形分成
条横线,便把正方形分成![]() 部分(如图③...如果在正方形中画
部分(如图③...如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线.便把正方形分成( )部分
条横线.便把正方形分成( )部分

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com