
分析 根据正比例与反比例的定义设出y与x之间的函数关系式,然后利用待定系数法求函数解析式计算即可得解.
解答 解:设y1=$\frac{{k}_{1}}{x}$,y2=k2(x+2),y=$\frac{{k}_{1}}{x}$+k2(x+2),(k1≠0,k2≠0),
将x=1、y=9和x=-1、y=-1分别代入,得$\left\{\begin{array}{l}{{k}_{1}+3{k}_{2}=9}\\{-{k}_{1}+{k}_{2}=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=3}\\{{k}_{2}=2}\end{array}\right.$.
故函数y与x的函数关系式为y=$\frac{3}{x}$+2(x+2).
点评 本题考查的是用待定系数法求反比例函数的解析式,是中学阶段的重点,一定要熟练掌握并灵活运用.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:填空题
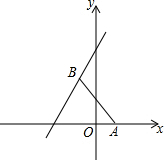 如图,点A的坐标为(1,0),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
如图,点A的坐标为(1,0),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
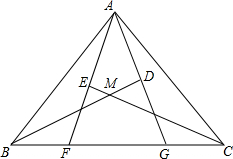 如图,△AFG中,BD、CE分别为AG、AF边的中垂线,交直线FG于点B、C,BD、CE交于点M,联结AB、AC,已知∠BAF=38°,∠CAG=22°,求∠BMC.
如图,△AFG中,BD、CE分别为AG、AF边的中垂线,交直线FG于点B、C,BD、CE交于点M,联结AB、AC,已知∠BAF=38°,∠CAG=22°,求∠BMC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com