
【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是 .(不再添加辅助线和字母)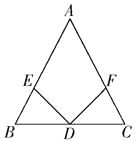
【答案】∠B=∠C(答案不唯一)。
【解析】试题分析:答案不唯一根据AB=AC,推出∠B=∠C,根据ASA证出△BED和△CFD全等即可;添加∠BED=∠CDF,根据AAS即可推出△BED和△CFD全等;根据∠AED=∠AFD推出∠B=∠C,根据ASA证△BED≌△CFD即可.
解:答案不唯一,如AB=AC或∠B=∠C或∠BED=∠CFD,或∠AED=∠AFD等;
理由是:①∵AB=AC,
∴∠B=∠C,
根据ASA证出△BED≌△CFD,即可得出DE=DF;
②由∠B=∠C,∠BDE=∠CDF,BD=DC,根据ASA证出△BED≌△CFD,即可得出DE=DF;
③由∠BED=∠CFD,∠BDE=∠CDF,BD=DC,根据AAS证出△BED≌△CFD,即可得出DE=DF;
④∵∠AED=∠AFD,∠AED=∠B+∠BDE,∠AFD=∠C+∠CDF,
又∵∠BDE=∠CDF,
∴∠B=∠C,
即由∠B=∠C,∠BDE=∠CDF,BD=DC,根据ASA证出△BED≌△CFD,即可得出DE=DF;
故答案为:答案不唯一,如AB=AC或∠B=∠C或∠BED=∠CFD或∠AED=∠AFD.


科目:初中数学 来源: 题型:
【题目】当m,n是实数且满足m﹣n=mn时,就称点Q(m, ![]() )为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y=
)为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y= ![]() 的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )
的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )
A.1
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高天然气使用效率,保障居民的本机用气需求,某地积极推进阶梯式气价改革,若一户居民的年用气量不超过300m3,价格为2.5元/m3,若年用气量超过300m3,超出部分的价格为3元/m3,
(1)根据题意,填写下表:

(2)设一户居民的年用气量为xm3,付款金额为y元,求y关于x的解析式;
(3)若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用5000元购进一批儿童玩具进行试销,很快销售一空.于是超市又调拨18000元资金购进该种儿童玩具,这次进货价比试销时每件多1元,购进的数量是试销时购进数量的3倍.
(1)求试销时该种儿童玩具每件进货价是多少元?
(2)超市将第二批儿童玩具按照试销时的标价出售90%后,余下的八折售完.试销和第二批儿童玩具两次销售中,超市总盈利不少于8520元,那么该种儿童玩具试销时每件标价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OE平分
,OE平分![]() ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点![]() 、B、C不与点O重合
、B、C不与点O重合![]() ,连接AC交射线OE于点
,连接AC交射线OE于点![]() 设
设![]() .
.

![]() 如图1,若
如图1,若![]() ,则
,则
![]() 的度数是______;
的度数是______;
![]() 当
当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______.
______.
![]() 如图2,若
如图2,若![]() ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得![]() 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
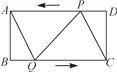
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,过点A作直线EF. 
(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com