
【题目】在等边△ABC外侧作直线AM,点C关于AM的对称点为D,连接BD交AM于点E,连接CE,CD,AD.
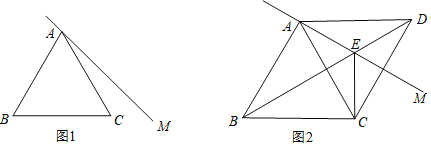
(1)依题意补全图1,并求∠BEC的度数;
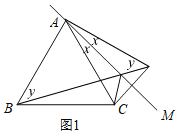
(2)如图2,当∠MAC=30°时,判断线段BE与DE之间的数量关系,并加以证明;
(3)若0°<∠MAC<120°,当线段DE=2BE时,直接写出∠MAC的度数.
【答案】(1)补全图形如图1所示,见解析,∠BEC=60°;(2)BE=2DE,见解析;(3)∠MAC=90°.
【解析】
(1)根据轴对称作出图形,先判断出∠ABD=∠ADB=y,再利用三角形的内角和得出x+y即可得出结论;
(2)同(1)的方法判断出四边形ABCD是菱形,进而得出∠CBD=30°,进而得出∠BCD=90°,即可得出结论;
(3)先作出EF=2BE,进而判断出EF=CE,再判断出∠CBE=90°,进而得出∠BCE=30°,得出∠AEC=60°,即可得出结论.
(1)补全图形如图1所示,
根据轴对称得,AD=AC,∠DAE=∠CAE=x,∠DEM=∠CEM.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∴AB=AD.
∴∠ABD=∠ADB=y.
在△ABD中,2x+2y+60°=180°,
∴x+y=60°.
∴∠DEM=∠CEM=x+y=60°.
∴∠BEC=60°;
(2)BE=2DE,
证明:∵△ABC是等边三角形,
∴AB=BC=AC,
由对称知,AD=AC,∠CAD=2∠CAM=60°,
∴△ACD是等边三角形,
∴CD=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,且∠BAD=2∠CAD=120°,
∴∠ABC=60°,
∴∠ABD=∠DBC=30°,
由(1)知,∠BEC=60°,
∴∠ECB=90°.
∴BE=2CE.
∵CE=DE,
∴BE=2DE.
(3)如图3,(本身点C,A,D在同一条直线上,为了说明∠CBD=90°,画图时,没画在一条直线上)
延长EB至F使BE=BF,
∴EF=2BE,
由轴对称得,DE=CE,
∵DE=2BE,
∴CE=2BE,
∴EF=CE,
连接CF,同(1)的方法得,∠BEC=60°,
∴△CEF是等边三角形,
∵BE=BF,
∴∠CBE=90°,
∴∠BCE=30°,
∴∠ACE=30°,
∵∠AED=∠AEC,∠BEC=60°,
∴∠AEC=60°,
∴∠MAC=180°﹣∠AEC﹣∠ACE=90°.



 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB=AC,
中,AB=AC,![]() ,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.
,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.

(1)∠EDB=_____![]() (用含
(用含![]() 的式子表示)
的式子表示)
(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转![]() ,与AC边交于点N.
,与AC边交于点N.
①根据条件补全图形;
②写出DM与DN的数量关系并证明;
③用等式表示线段BM、CN与BC之间的数量关系,(用含![]() 的锐角三角函数表示)并写出解题思路.
的锐角三角函数表示)并写出解题思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO,线段OP,连结BP,动点M在线段AP⊥(点M与点F、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
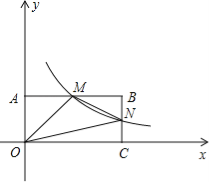
【题目】如图,点A(a,b)是双曲线y=![]() (x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于C点,过A作AD⊥x轴于D点,连接AP交y轴于B点.
(x>0)上的一点,点P是x轴负半轴上的一动点,AC⊥y轴于C点,过A作AD⊥x轴于D点,连接AP交y轴于B点.
(1)△PAC的面积是 ;
(2)当a=2,P点的坐标为(﹣2,0)时,求△ACB的面积;
(3)当a=2,P点的坐标为(x,0)时,设△ACB的面积为S,试求S与x之间的函数关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
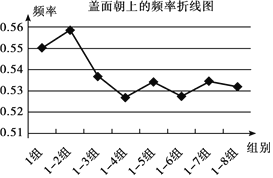
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】豆豆妈妈用小米运动手环记录每天的运动情况,下面是她6天的数据记录(不完整):
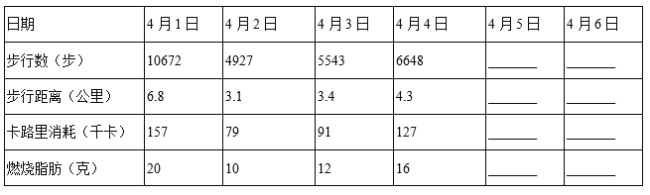
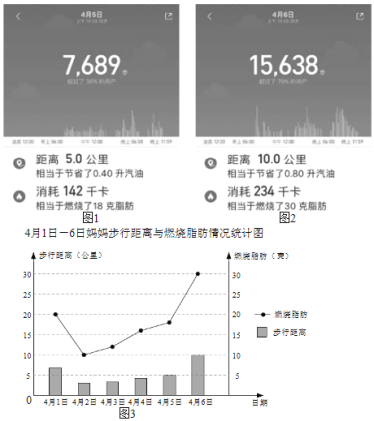
(1)4月5日,4月6日,豆豆妈妈没来得及作记录,只有手机图片,请你根据图片数据,帮她补全表格.
(2)豆豆利用自己学习的统计知识,把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来,请你根据图中提供的信息写出结论: .(写一条即可)
(3)豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系,豆豆妈妈想使自己的卡路里消耗数达到250千卡,预估她一天步行距离为 公里.(直接写出结果,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.

① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+ ![]() (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).
(2)【解决问题】
直接写出“问题情境”中问题的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在开展“太极拳进校园”活动,为了解学生太极拳的练习情况,随机抽取了部分学校学生进行问卷调查,将调查结果按照“![]() 每周练习6次或7次,
每周练习6次或7次,![]() 每周练习4次或5次,
每周练习4次或5次,![]() 每周练习2次或3次,
每周练习2次或3次,![]() 每周练习0次或1次”四类分别进行统计,并绘制了下列两幅尚不完整的统计图.
每周练习0次或1次”四类分别进行统计,并绘制了下列两幅尚不完整的统计图.
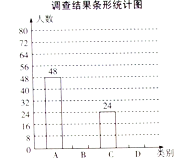
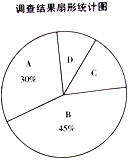
请根据图中信息,解答下列问题:
(1)此次共调查了___________名学生;
(2)在扇形统计图中,扇形![]() 的圆心角度数为__________;
的圆心角度数为__________;
(3)请将条形统计图补充完整;
(4)若该市约有30万名学生,请你估计每周练习太极拳不少于4次的学生的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com