Question

【题目】已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．

（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．

①求证：△OCP∽△PDA；

②若△OCP与△PDA的面积比为1：4，求边AB的长．

（2）若图1中的点P恰好是CD边的中点，求∠OAB的度数；

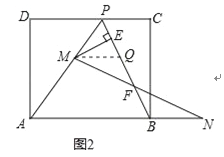
（3）如图2，在（1）的条件下，擦去折痕AO，线段OP，连结BP，动点M在线段AP⊥（点M与点F、A不重合），动点N在线段AB的延长线上，且BN=PM，连结MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；说明理由；若不变，求出线段EF的长度．

Answer 1

【答案】见解析

【解析】

（1）①根据折叠的性质得到∠APO=∠B=90°，根据相似三角形的判定定理证明△OCP∽△PDA；

②根据相似三角形的面积比等于相似比的平方解答；

（2）根据直角三角形的性质得到∠DAP=30°，根据折叠的性质解答即可；

（3）作MQ∥AB交PB于Q，根据等腰三角形的性质和相似三角形的性质得到EF=PB，根据勾股定理求出PB，计算即可．

解：（1）①由折叠的性质可知，∠APO=∠B=90°，

∴∠APD+∠OPC=90°，又∠POC+∠OPC=90°，

∴∠APD=∠POC，又∠D=∠C=90°，

∴△OCP∽△PDA；

②∵△OCP与△PDA的面积比为1：4，

∴△OCP与△PDA的相似比为1：2，

∴PC=AD=4，

设AB=x，则DC=x，AP=x，DP=x﹣4，

在Rt△APD中，AP2=AD2+PD2，即x2+82=（x﹣4）2，

解得，x=10，即AB=10；

（2）∵点P是CD边的中点，

∴DP=DC，又AP=AB=CD，

∴DP=AP，

∴∠DAP=30°，

由折叠的性质可知，∠OAB=∠OAP=30°；

（3）EF的长度不变．

作MQ∥AB交PB于Q，

∴∠MQP=∠ABP，

由折叠的性质可知，∠APB=∠ABP，

∴∠MQP=∠APB，

∴MP=MQ，又BN=PM，

∴MQ=BN，

∵MQ∥AB，

∴，

∴QF=FB，

∵MP=MQ，ME⊥BP，

∴PE=QE，

∴EF=PB，

由（1）得，PC=4，BC=8，

∴PB==4，

∴EF=2．