
【题目】已知![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.15°或
B.15°或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】A
【解析】
根据题意画出图形,分两种情况讨论:∠BOC在∠AOB内部和外部;当∠BOC在∠AOB内部时,根据角平分线的定义以及角的和差可得∠MON=∠AOM∠AON,当∠BOC在∠AOB外部时可得∠MON=∠AON-∠AOM.
解:如图所示,当∠BOC在∠AOB内部时,
∵∠AOB=80°,其角平分线为OM,
∴∠AOM=40°,
∵∠BOC=30°,
∴∠AOC=50°,
∵![]() 平分
平分![]() ,
,
∴∠AON=25°,
∴∠MON=∠AOM∠AON=40°25°=15°;
如图所示,当∠BOC在∠AOB外部时,

∵∠AOB=80°,其角平分线为OM,
∴∠AOM=40°,
∵∠BOC=30°,
∴∠AOC=110°,
∵![]() 平分
平分![]() ,
,
∴∠AON=55°,
∴∠MON=∠AON-∠AOM=55°-40°=15°.
故选A.


科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程.
如图,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() .
.

(1)求![]() 的度数:
的度数:
(2)如果![]() ,求
,求![]() 的度数.
的度数.
解:(1)如图,因为![]() 是
是![]() 的平分线,
的平分线,
所以![]() .
.
因为![]() 是
是![]() 的平分线,
的平分线,
所以![]() ① .
① .
所以![]() ②
② ![]() ③
③ ![]() .
.
(2)由(1)可知![]() .
.
因为![]()
所以 ④ ![]()
则:![]() ⑤
⑤ ![]() ⑥
⑥ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
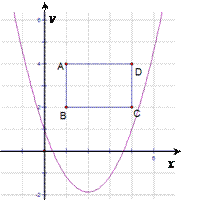
【题目】如图,二次函数![]() 的图象经过点(0,1)坐标平面内有矩形ABCD,A(1,4),B(1,2)C(4,2),D(4,4)
的图象经过点(0,1)坐标平面内有矩形ABCD,A(1,4),B(1,2)C(4,2),D(4,4)
(1)用a表示k;
(2)试说明抛物线图象一定经过(4,1);
(3)求抛物线顶点在x轴上方时,a的取值范围;
(4)写出抛物线与矩形ABCD各边交点个数与a的对应取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | |
甲 | ______________ | 8 | 8 |
乙 | ______________ | 9 | ______________ |
(2)已知甲组学生成绩的方差![]() ,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO,线段OP,连结BP,动点M在线段AP⊥(点M与点F、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN于点E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简:
(1)3b+5a-(2a-4b )
(2)化简求值:7a2b+2(2a2b-3ab2)-(4a2b-ab2),其中a,b满足|a+2|+(b![]() )2 =0
)2 =0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com