
【题目】已知数轴上两点![]() 对应的数分别是
对应的数分别是![]() ,
,![]() ,
,![]() 为数轴上三个动点,点
为数轴上三个动点,点![]() 从
从![]() 点出发速度为每秒
点出发速度为每秒![]() 个单位,点
个单位,点![]() 从点
从点![]() 出发速度为
出发速度为![]() 点的
点的![]() 倍,点
倍,点![]() 从原点出发速度为每秒
从原点出发速度为每秒![]() 个单位.
个单位.

![]() 若点
若点![]() 向右运动,同时点
向右运动,同时点![]() 向左运动,求多长时间点
向左运动,求多长时间点![]() 与点
与点![]() 相距
相距![]() 个单位?
个单位?
![]() 若点
若点![]() 同时都向右运动,求多长时间点
同时都向右运动,求多长时间点![]() 到点
到点![]() 的距离相等?
的距离相等?
【答案】(1)5秒;(2)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)设经过x秒点M与点N相距54个单位,由点M从A点出发速度为每秒2个单位,点N从点B出发速度为M点的3倍,得出2x+6x+14=54求出即可;
(2)首先设经过t秒点P到点M,N的距离相等,得出(2t+6)-t=(6t-8)-t或(2t+6)-t=t-(6t-8),进而求出即可.
解:(1)设经过x秒点M与点N相距54个单位.
依题意可列方程为:2x+6x+14=54,
解方程,得x=5.
∴经过5秒点![]() 与点
与点![]() 相距
相距![]() 个单位.
个单位.
(2)设经过t秒点P到点M,N的距离相等.
(2t+6)-t=(6t-8)-t或(2t+6)-t=t-(6t-8),
t+6=5t-8或t+6=8-5t
![]() 或
或![]()
∴经过![]() 秒或
秒或![]() 秒点
秒点![]() 到点
到点![]() 的距离相等
的距离相等


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO,线段OP,连结BP,动点M在线段AP⊥(点M与点F、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
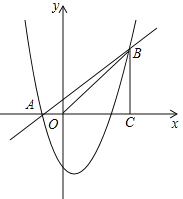
【题目】如图,已知抛物线![]() 经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)写出该厂星期一生产工艺品的数量;
(2)本周产量最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() 点是底边
点是底边![]() 上的一个动点,
上的一个动点,![]() ,
,![]() .
.
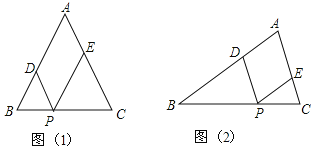
(1)用![]() 表示四边形
表示四边形![]() 的周长为 ;
的周长为 ;
(2)点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形,请说明理由;
是菱形,请说明理由;
(3)如果![]() 不是等腰三角形图(2),其他条件不变,点
不是等腰三角形图(2),其他条件不变,点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形(不必说明理由).
是菱形(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简:
(1)3b+5a-(2a-4b )
(2)化简求值:7a2b+2(2a2b-3ab2)-(4a2b-ab2),其中a,b满足|a+2|+(b![]() )2 =0
)2 =0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用四根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )

A. ∠A=∠CB. ∠ABC=∠CDA
C. ∠ABD=∠CDBD. ∠ABC=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6.
求:(1)求这个矩形对角线的长;
(2)BC的长;
(3)矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(﹣6,0),D(﹣7,3),点B、C在第二象限内.
(1)求点B的坐标。
(2)将正方形ABCD以每秒1个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在x轴上的点P和反比例函数图象上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com