
分析 分两种情况探讨:点A落在矩形对角线BD上,点A落在矩形对角线AC上,在直角三角形中利用勾股定理列出方程,通过解方程可得答案.
解答 解:,①点A落在矩形对角线BD上,如图1,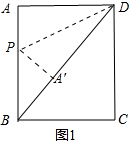
∵AB=16,BC=12,
∴BD=20,
根据折叠的性质,AD=A′D=12,AP=A′P,∠A=∠PA′D=90°,
∴BA′=8,
设AP=x,则BP=16-x,
∵BP2=BA′2+PA′2,
∴(16-x)2=x2+82,
解得:x=6,
∴AP=6;
②点A落在矩形对角线AC上,如图2,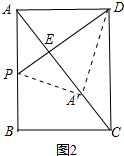
根据折叠的性质可知DP⊥AC,
∴△DAP∽△ABC,
∴$\frac{AD}{AP}$=$\frac{AB}{BC}$,
AP=$\frac{AD•BC}{AB}$=9,
故答案为:②④.
点评 本题考查了折叠问题、勾股定理,矩形的性质以及三角形相似的判定与性质;解题中,找准相等的量是正确解答题目的关键.


科目:初中数学 来源: 题型:选择题
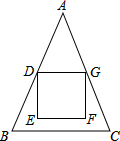 如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )| A. | 1 | B. | 2 | C. | $\sqrt{21}$ | D. | $\sqrt{29}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
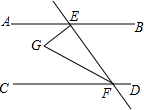 如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )
如图,AB∥CD,EF与AB,CD分别交于点E,F,EG⊥EF,与∠EFC的平分线FG交于点G.若∠EFG=25°,则∠AEG的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
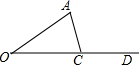 如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.
如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:| 2011届 | 2012届 | 2013届 | 2014届 | 2015届 | |
| 参与实验的人数 | 106 | 110 | 98 | 104 | 112 |
| 右手大拇指在上的人数 | 54 | 57 | 49 | 51 | 56 |
| 频率 | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
| A. | 0.6 | B. | 0.5 | C. | 0.45 | D. | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
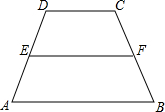 如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com