练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
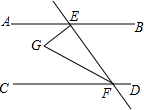
    13．如图，AB∥CD，EF与AB，CD分别交于点E，F，EG⊥EF，与∠EFC的平分线FG交于点G．若∠EFG=25°，则∠AEG的大小为（　　）
    A．30°B．40°C．50°D．60°

    分析 先根据角平分线的性质求出∠EFC的度数，再由平行线的性质得出∠AEF的度数，根据EG⊥EF得出∠GEF=90°，进而可得出结论．

    解答 解：∵FG是∠EFC的平分线，∠EFG=25°，
    ∴∠EFC=2∠EFG=50°．
    ∵AB∥CD，
    ∴∠AEF=180°-∠EFC=180°-50°=130°．
    ∵EG⊥EF，
    ∴∠GEF=90°，
    ∴∠AEG=∠AEF-∠GEF=130°-90°=40°．
    故选B．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

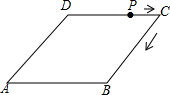    3．如图，菱形ABCD的边长为4，∠A=30°，点P从起点D出发，沿DC、CB向终点B匀速运动．设点P所走过的路程为x，△ADP的面积为y，则y关于x的函数图象是（　　）
    A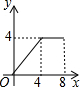．B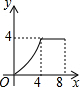．C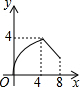．D．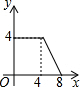

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知n为正整数，且x2n=4，求（x3n）2-2（x2）2n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

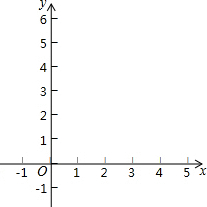    1．在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴相交于点A和点B，已知点A的坐标为（1，0），与y轴相交于点C（0，3），抛物线的顶点为P．
    （1）求这条抛物线的解析式，并写出顶点P的坐标；
    （2）如果点D在此抛物线上，DF⊥x轴于点F，DF与直线PB相交于点E，设点D的横坐标为t（t＞3），且DE：EF=2：1，求点D的坐标；
    （3）在第（2）小题的条件下，求证：∠DPE=∠BDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先化简，再求值：$\frac{a}{{a}^{2}-{b}^{2}}-\frac{b}{{a}^{2}-{b}^{2}}$，其中a=2，b=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．一元二次方程3x2+5x+1=0有实数根．（填“有”或“没有”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．解方程：
    （1）$\frac{2}{x+1}$-$\frac{1}{x}$=0             
    （2）$\frac{x-2}{x+2}$-$\frac{16}{{x}^{2}-4}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．在矩形纸片ABCD中，AB=16，AD=12，点P在边AB上，若将△DAP沿DP折叠，使点A恰好落在矩形对角线上的点A′处，则AP的长可能为②④．（把所有正确结论的序号都选上）
    ①5；②6；③8；④9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

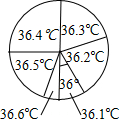    3．为了解九（1）班学生的体温情况，对这个班所有学生测量了一次体温（单位：℃），小明将测量结果绘制成如下统计表和如图所示的扇形统计图．下列说法错误的是（　　）
    体温（℃）36.136.236.336.436.536.6
    人数（人）48810x2
    A．这些体温的众数是8B．这些体温的中位数是36.35
    C．这个班有40名学生D．x=8

    查看答案和解析>>

    同步练习册答案