
 如图在⊙O中,AC=BC,OD=OE,求证:∠ACD=∠BCE.
如图在⊙O中,AC=BC,OD=OE,求证:∠ACD=∠BCE. ∠AOC=∠BOC,
∠AOC=∠BOC,
|
|


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
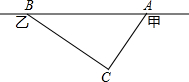 在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.
在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.查看答案和解析>>
科目:初中数学 来源: 题型:
 在如图所示的网格中,已知A(2,4),B(4,2),点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
在如图所示的网格中,已知A(2,4),B(4,2),点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
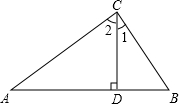 如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是
如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是| CD |
| AD |
| DB |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com