练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某游乐场试营业期间，每天运营成本为1000元.经统计发现，每天售出的门票张数（张）与门票售价（元/张）之间满足一次函数，设游乐场每天的利润为（元）.（利润=票房收入－运营成本）

    （1）试求与之间的函数表达式.

    （2）游乐场将门票售价定为多少元/张时，每天获利最大？最大利润是多少元？

    【答案】（1）w=;（2）游乐场将门票售价定为25元/张时，每天获利最大，最大利润是1500元

    【解析】

    （1）根据及利润=票房收入－运营成本即可得出化简即可.

    （2）根据二次函数的性质及对称轴公式即可得最大值，及x的值.

    （1）根据题意，得.

    （2）∵中，，

    ∴有最大值.

    当时，最大，最大值为1500.

    答：游乐场将门票售价定为25元/张时，每天获利最大，最大利润是1500元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,若果∠1＝∠2，那么添加下列任何一个条件：（1），（2），（3）∠B＝∠D，（4）∠C＝∠AED， 其中能判定△ABC∽△ADE的个数为

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知线段， 是上的一动点，是的中点，以为边作正方形，点关于射线的对称点为 ，连接、，直线交于点．

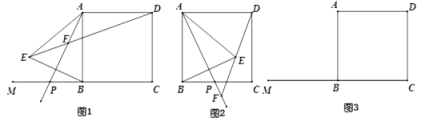
    （1）如图1，当点在线段上，且，求的度数；

    （2）小明在解题时发现：当点在线段上时，线段，，之间满足，那么你认为当点在线段上时（如图2），他的结论是否还成立？若成立，请证明，若不成立，请说明理由；

    （3）如图3，点在上，且，当点从点运动到点时，直接写出点所经过的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图1，在中，把绕点逆时针旋转（）并延长一倍得到，把绕点顺时针旋转并延长一倍得到，连接．当时，称是的“倍旋三角形”，边上的中线叫做的“倍旋中线”．

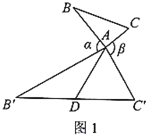
    特例感知：

    （1）如图1，当，时，则“倍旋中线”长为______；如图2，当为等边三角形时，“倍旋中线”与的数量关系为______；

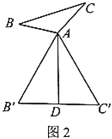
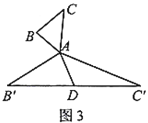
    猜想论证：

    （2）在图3中，当为任意三角形时，猜想“倍旋中线”与的数量关系，并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准，共支付两种垃圾处理费5000元，从去年元月起，收费标准上调为：可回收垃圾处理费30元/吨，不可回收垃圾处理费100元/吨．若该企业去年处理的这两种垃圾数量与前年相比没有变化，但调价后就要多支付处理费9000元．

    （1）该企业前年处理的可回收垃圾和不可回收垃圾各多少吨？

    （2）该企业计划今年将上述两种垃圾处理总量减少到200吨，且可回收垃圾不少于不可回收垃圾处理量的3倍，则今年该企业至少有多少吨可回收垃圾？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】改革开放以来，由于各阶段发展重心不同，某市的需求结构经历了消费投资交替主导、投资消费双轮驱动到消费主导的变化.到2007年，某市消费率超过投资率，标志着某市经济增长由投资消费双轮驱动向消费趋于主导过渡．下图是某市1978—2017年投资率与消费率统计图.根据统计图回答：________年，某市消费率与投资率相同；从2000年以后，某市消费率逐年上升的时间段是________．

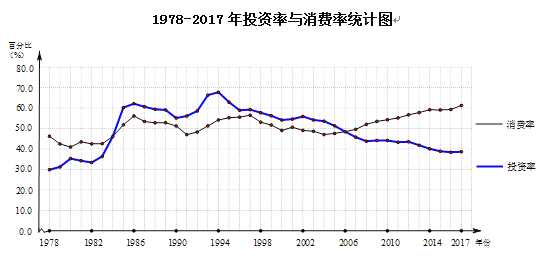
    查看答案和解析>>

    科目：初中数学 来源： 题型：

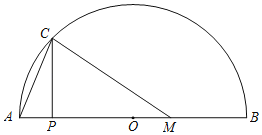
    【题目】如图，在半圆弧AB中，直径AB＝6cm，点M是AB上一点，MB＝2cm，P为AB上一动点，PC⊥AB交AB于点C，连接AC和CM，设A、P两点间的距离为xcm，A、C两点间的距离为y1cm，C、M两点间的距离为y2cm．

    小东根据学习函数的经验，分别对函数y1、y2随自变量x的变化而变化的规律进行了探究：

    下面是小东的探究过程，请补充完整：

    （1）按照下表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值；

    x/cm

    0

    1

    2

    3

    4

    5

    6

    y1/cm

    0

    2.45

    3.46

    4.90

    5.48

    6

    y2/cm

    4

    3.74

    3.46

    3.16

    2.83

    2.45

    2

    （2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；

    （3）结合函数图象，解决问题：

    ①当AC＞CM时，线段AP的取值范围是　 　；

    ②当△AMC是等腰三角形时，线段AP的长约为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

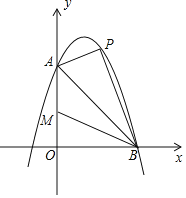
    【题目】如图，已知抛物线与y轴交于点，与x轴交于点，点P是线段AB上方抛物线上的一个动点．

    求这条抛物线的表达式及其顶点坐标；

    当点P移动到抛物线的什么位置时，使得，求出此时点P的坐标；

    当点P从A点出发沿线段AB上方的抛物线向终点B移动，在移动中，点P的横坐标以每秒1个单位长度的速度变动；与此同时点M以每秒1个单位长度的速度沿AO向终点O移动，点P，M移动到各自终点时停止当两个动点移动t秒时，求四边形PAMB的面积S关于t的函数表达式，并求t为何值时，S有最大值，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

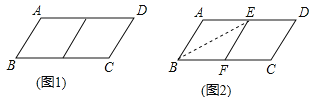
    【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依次类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形中，若，则平行四边形为1阶准菱形．

    （1）判断与推理：

    ① 邻边长分别为2和3的平行四边形是__________阶准菱形；

    ② 小明为了剪去一个菱形，进行如下操作：如图2，把平行四边形沿着折叠（点在上）使点落在边上的点，得到四边形，请证明四边形是菱形．

    （2）操作、探究与计算：

    ① 已知平行四边形的邻边分别为1，裁剪线的示意图，并在图形下方写出的值；

    ② 已知平行四边形的邻边长分别为，满足，请写出平行四边形是几阶准菱形．

    查看答案和解析>>

    同步练习册答案