
����Ŀ���Ķ����ϣ�
���Ƕ��壺���һ������ƽ�����ک�1������i2=��1����ô���i�ͽ���������λ������������ѧ����ʵ������һ�����������һ���������Ա�ʾΪa+bi��a��b��Ϊʵ��������ʽ������a��������ʵ����b���������鲿��
�����ļӡ������˵�����������ѧ������ʽ�ӡ������˵��������ƣ�
���� ���㣺��5+i��+��3��4i��=��5+3��+��i��4i��=8��3i��
�����������ϣ�����������⣺
��1����գ�i3=�� ����i4=�� ����
��2�����㣺��2+i��2��
��3����![]() ��Ϊa+bi��a��b��Ϊʵ��������ʽ������Ϊ��ĸ�в���i����ʽ����
��Ϊa+bi��a��b��Ϊʵ��������ʽ������Ϊ��ĸ�в���i����ʽ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ�AD���ӳ�����BC���ӳ����ཻ�ڵ�E��DC=DE�� 
��1����֤����A=��AEB��
��2�����DC��OE����֤����ABE�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�OΪ����ABCD�ĶԳ����ģ���֪C��2��0����D��0����1����NΪ�߶�CD��һ�㣨����C��D�غϣ���
��1������CΪ���㣬�Ҿ�����D�������߽���ʽ��
��2����N����BD�ĶԳƵ�ΪN1 �� N����BC�ĶԳƵ�ΪN2 �� ��֤����N1BN2�ס�ABC��
��3����2����N1N2����Сֵ��
��4������N��y���ƽ���߽���1���е��������ڵ�P����QΪֱ��AB�ϵ�һ�����㣬�ҡ�PQA=��BAC����PQ��Сʱ��Q���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��AB����CD�ཻ�ڵ�E��AB��CD����O������BF����AD���ӳ����ཻ�ڵ�F������O�İ뾶Ϊ5��cos��BCD= ![]() ����ô�߶�AD= ��
����ô�߶�AD= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ҹ���������������������û����ͽ��������Ϊ���㣮Ϊ�˵���ѧ������������֪ʶ���˽�̶ȣ�ijУ��ѧ��������һ�γ������飬����������Ϊ�ĸ��ȼ���A���dz��˽⣻B���Ƚ��˽⣻C�������˽⣻D�����˽⣮���ݵ���ͳ�ƽ���������˲�����������ͳ��ͼ���� �������˽�̶ȵ�ͳ�Ʊ���
���������˽�̶� | �ٷֱ� |
A���dz��˽� | 5% |
B���Ƚ��˽� | m |
C�������˽� | 45% |
D�����˽� | n |
����ͳ��ͼ�����ش��������⣮
�����������˽�̶ȵ�����ͳ��ͼ
�����������˽�̶ȵ�����ͳ��ͼ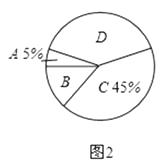
��1�����β�������ѧ�������ˣ�m= �� n=��
��2��ͼ2��ʾ������ͳ��ͼ��D������������Ӧ��Բ�Ľ����ȣ�
��3���벹ȫͼ1ʾ��������ͳ��ͼ��
��4�����ݵ�������ѧУ����չ��������֪ʶ������ij��Ҫ�ӡ��dz��˽⡱̬�ȵ�С����С����ѡһ�˲μӣ��������������Ϸ��ȷ������������ǣ����ĸ���ȫ��ͬ��ƹ�����������1��2��3��4��Ȼ��ŵ�һ�������Ĵ��У�һ�����ȴӴ����������һ������һ���ٴ�ʣ�µ����������������һ�������������������ϵ����ֺ�Ϊ��������С��ȥ������С��ȥ��������״ͼ���б���˵�������Ϸ�����Ƿ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪����A��0��0����B�� ![]() ��0����C��0��1���ڡ�ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1 �� ��2����B1A2B2 �� ��3����B2A3B3 �� �������n���ȱ������εı߳����� ��
��0����C��0��1���ڡ�ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1 �� ��2����B1A2B2 �� ��3����B2A3B3 �� �������n���ȱ������εı߳����� �� 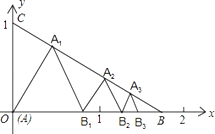
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=2x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��D������AB�ϵĶ��㣨�����A�غϣ���DN��x����N���ѡ�AND��ֱ��AB���ۣ��õ���AMD���ӳ�MA��y���ڵ�C����A��C��D�����ԲE��x�ύ�ڵ�F������DF�� 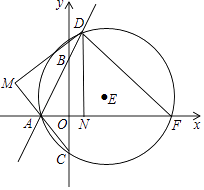
��1��ֱ��д��tan��BAO��ֵΪ��
��2����֤��MC=NF��
��3�����߶�OC�ij���
��4���Ƿ���ڵ�D��ʹDF��AC�������ڣ����D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ڽ��ڡ�O��P���ӻ�BC������һ�㣬PA��BC���ڵ�E�������½��ۣ���PA=PB+PC���� ![]() ����PAPE=PBPC�����У���ȷ���۵ĸ���Ϊ�� ��
����PAPE=PBPC�����У���ȷ���۵ĸ���Ϊ�� �� 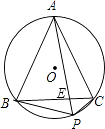
A.3��
B.2��
C.1��
D.0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ�յ����ڵ�С���ڸ�������£������������ɽ���硢�ȳǽ��塢������������ѡ��һ�����㣬�������ͩ���ơ�÷ɳ̤�ˡ�һ�����������ѡ��һ�����㣬С��ǡ������ѡ����ɽ���磬����ѡ��÷ɳ̤�˵ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com