练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，反比例函数y＝的图象与一次函数y＝kx+b的图象交于A，B两点，

    点A的坐标为(2，6)，点B的坐标为(n，1)．

    (1)求反比例函数与一次函数的表达式；

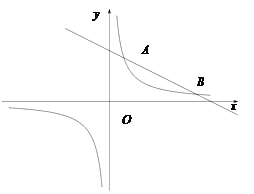
    (2)点E为y轴上一个动点，若S△AEB＝10，求点E的坐标．

    【答案】（1）y＝x+7　　（2）(0，5)或(0，9)．

    【解析】

    解：(1)把点A(2，6)代入y＝，得m＝12，则y＝．

    把点B(n，1)代入y＝，得n＝12，则点B的坐标为(12，1)．

    由直线y＝kx+b过点A(2，6)，点B(12，1)得，解得，

    则所求一次函数的表达式为y＝x+7．

    (2)如图所示，

    直线AB与y轴的交点为P，设点E的坐标为(0，m)，连接AE，BE，

    则点P的坐标为(0，7)．∴PE＝|m－7|．

    ∵S△AEB＝S△BEP－S△AEP＝10，∴×|m－7|×(12－2)＝10．

    ∴|m－7|＝2．∴m1＝5，m2＝9．

    ∴点E的坐标为(0，5)或(0，9)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

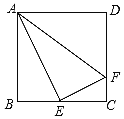
    【题目】如图，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF＝CD，下列结论中错误的是（　　）

    A.B.△ABE∽△AEF

    C.△ABE∽△ECFD.△ADF∽△ECF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

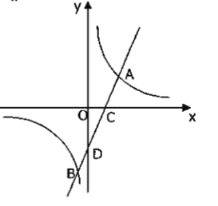
    【题目】如图，已知点，在反比例函数的图象上，直线分别与轴、轴相交于、两点.

    （1）求直线的解析式：

    （2）求、两点坐标；

    （3）连接、，记的面积为、面积为，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个二次函数图象的顶点坐标为（-1,2），于y轴交点的纵坐标为

    （1）求这个二次函数的表达式；

    （2）在给定的直角坐标系中，画出这个函数的图象；

    （3） 已知两点A（-2020，a），B（2019，b）在此二次函数图象上，请比较a与b的大小。a b（用＞，＝或＜填空）

    （4）根据图像，当-2＜x＜2时，请直接写出y的取值范围　 　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等边△ABC中，D是AC边上一点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED，若BC=5，BD=4，有下列结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△ADE的周长是9.其中正确的个数是（ ）

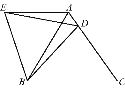
    A. 4 B. 3 C. 2 D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，抛物线y＝﹣x2﹣x﹣3交x轴于A，B两点（点A在点B的左侧），交y轴于点C

    （1）求直线AC的解析式；

    （2）点P是直线AC上方抛物线上的一动点（不与点A，点C重合），过点P作PD⊥x轴交AC于点D，求PD的最大值；

    （3）将△BOC沿直线BC平移，点B平移后的对应点为点B′，点O平移后的对应点为点O′，点C平移后的对应点为点C′，点S是坐标平面内一点，若以A，C，O′，S为顶点的四边形是菱形，求出所有符合条件的点S的坐标．

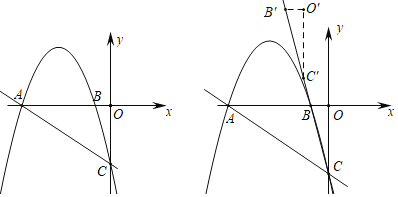
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在甲、乙两座楼正中间有一堵院墙，小明站在甲楼某层窗口前，同时小光站在乙楼某层窗口前观察这堵墙，小明视线所及位置如图所示，小光视线恰好落在甲楼底部．已知墙的高度为5米，两栋楼的间距为100米，小明视线所及位置到墙的距离为10米．

    （1）请根据题意画出平面图形，并标上相应字母．

    （2）求甲、乙两人的观测点到地面高度的距离差．

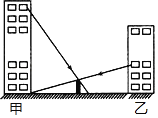
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线MN与x轴、y轴分别交于A、C两点，分别过A、C两点作x轴、y轴的垂线相交于B点，且OA、OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48＝0的两个实数根．

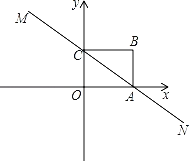
    （1）求A、C两点的坐标．

    （2）求直线MN的表达式．

    （3）在直线MN上存在点P，使以点P、B、C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

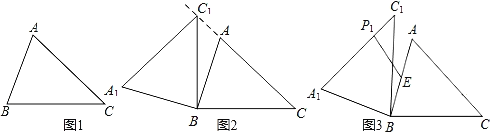
    【题目】如图1，在锐角△ABC中，AB＝5，AC＝4，∠ACB＝45°

    （1）计算：求BC的长；

    （2）操作：将图1中的△ABC绕点B按逆时针方向旋转，得到△A1BC1．如图2，当点C1在线段CA的延长线上时．

    ①求∠CC1A1的度数；

    ②求四边形A1BCC1的面积；

    （3）探究：如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转所得到的△A1BC1中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．

    查看答案和解析>>

    同步练习册答案