
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=![]() CD,下列结论中错误的是( )
CD,下列结论中错误的是( )
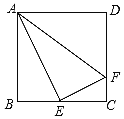
A.![]() B.△ABE∽△AEF
B.△ABE∽△AEF
C.△ABE∽△ECFD.△ADF∽△ECF
【答案】D
【解析】
推导出∠B=∠C=90°,AB:EC=BE:CF=2:1,从而△ABE∽△ECF,故EF=![]() AE,进而∠AEF=∠B=90°,由此能得到△ABE∽△AEF,AE⊥EF.
AE,进而∠AEF=∠B=90°,由此能得到△ABE∽△AEF,AE⊥EF.
解:∵在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=![]() CD,
CD,
∴∠B=∠C=90°,AB:EC=BE:CF=2:1.
∴△ABE∽△ECF.
∴AB:EC=AE:EF=2:1,∠AEB=∠EFC.
∵BE=CE,∠FEC+∠EFC=90°,
∴AB:AE=BE:EF,∠AEB+∠FEC=90°.
∴∠AEF=∠B=90°.
∴△ABE∽△AEF.
∴A,B,C正确.
在△ADF和△ECF中,两直角边的对应比不相等,故△ADF和△ECF不相似.
故选:D.


科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的柑橘,物价部门规定每箱售价不得高于55元;市场调查发现,若每箱以45元的价格销售,平均每天销售105箱;每箱以50元的价格销售,平均每天销售90箱.假定每天销售量y(箱)与销售价x(元/箱)之间满足一次函数关系式.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
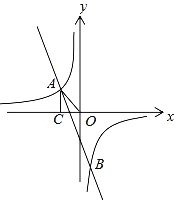
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(m,4)、B(2,﹣6)两点,过A作AC⊥x轴交于点C,连接OA.
的图象相交于A(m,4)、B(2,﹣6)两点,过A作AC⊥x轴交于点C,连接OA.
(1)分别求出一次函数与反比例函数的表达式;
(2)若直线AB上有一点M,连接MC,且满足S△AMC=3S△AOC,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一幅长为90cm,宽为60cm的有关北京东奥会的长方形宣传画.
(1)为测量宣传画上吉祥物冰墩墩的面积,现将宣传画平铺在地上,向长方形宣传画内随机投掷骰子(假设骰子落在长方形内的每一点都是等可能的),经过大量重复投掷试验,发现骰子落在吉祥物冰墩墩中的频率稳定在常数0.4附近,由此可估计宣传画上吉祥物冰墩墩的面积约为 cm2;
(2)若要为此宣传画配一个镜框制成一幅矩形挂画,要求镜框的四条边宽度相等.如果要使整个挂画的面积为7000cm2,那么镜框边的宽度应是多少厘米?

查看答案和解析>>
科目:初中数学 来源: 题型:
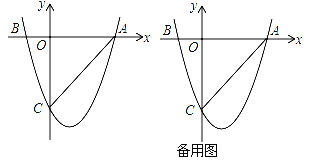
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
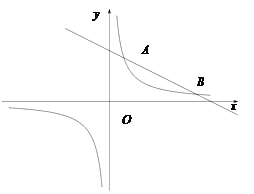
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,
的图象与一次函数y=kx+b的图象交于A,B两点,
点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com